 | ||
An N×N Euclidean random matrix  is defined with the help of an arbitrary deterministic function f(r, r′) and of N points {ri} randomly distributed in a region V of d-dimensional Euclidean space. The element Aij of the matrix is equal to f(ri, rj): Aij = f(ri, rj).
Contents
History
Euclidean random matrices were first introduced in 1999. They studied a special case of functions f that depend only on the distances between the pairs of points: f(r, r′) = f(r - r′) and imposed an additional condition on the diagonal elements Aii,
Aij = f(ri - rj) - u δij∑kf(ri - rk),motivated by the physical context in which they studied the matrix. A Euclidean distance matrix is a particular example of Euclidean random matrix with either f(ri - rj) = |ri - rj|2 or f(ri - rj) = |ri - rj|.
For example, in many biological networks, the strength of interaction between two nodes depends on the physical proximity of those nodes. Spatial interactions between nodes can be modelled as a Euclidean random matrix, if nodes are placed randomly in space.
Properties
Because the positions of the points {ri} are random, the matrix elements Aij are random too. Moreover, because the N×N elements are completely determined by only N points and, typically, one is interested in N≫d, strong correlations exist between different elements.
Hermitian Euclidean random matrices
Hermitian Euclidean random matrices appear in various physical contexts, including supercooled liquids, phonons in disordered systems, and waves in random media.
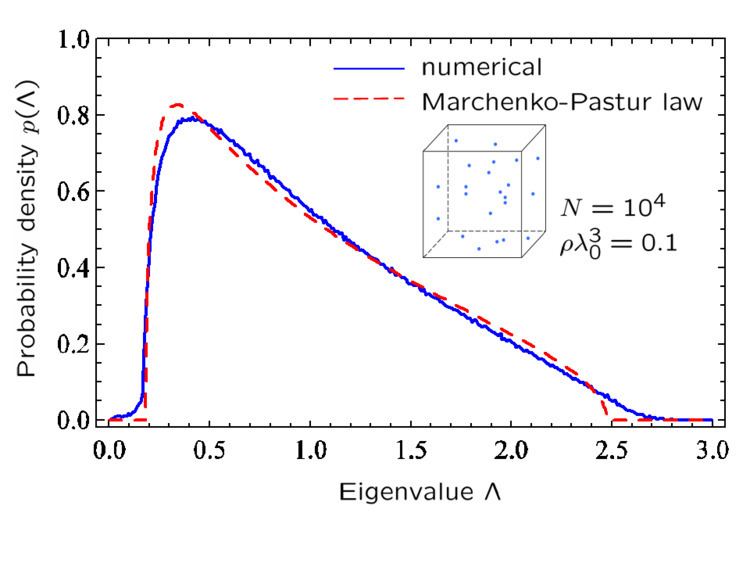
Example 1: Consider the matrix  generated by the function f(r, r′) = sin(k0|r-r′|)/(k0|r-r′|), with k0 = 2π/λ0. This matrix is Hermitian and its eigenvalues Λ are real. For N points distributed randomly in a cube of side L and volume V = L3, one can show that the probability distribution of Λ is approximately given by the Marchenko-Pastur law, if the density of points ρ = N/V obeys ρλ03 ≤ 1 and 2.8N/(k0 L)2 < 1 (see figure).
Non-Hermitian Euclidean random matrices
A theory for the eigenvalue density of large (N≫1) non-Hermitian Euclidean random matrices has been developed and has been applied to study the problem of random laser.
Example 2: Consider the matrix  generated by the function f(r, r′) = exp(ik0|r-r′|)/(k0|r-r′|), with k0 = 2π/λ0 and f(r= r′) = 0. This matrix is not Hermitian and its eigenvalues Λ are complex. The probability distribution of Λ can be found analytically if the density of point ρ = N/V obeys ρλ03 ≤ 1 and 9N/(8k0 R)2 < 1 (see figure).
