Error threshold (evolution)

Fitness landscape

It was noted by Manfred Eigen in his 1971 paper (Eigen 1971) that this mutation process places a limit on the number of digits a molecule may have. If a molecule exceeds this critical size, the effect of the mutations become overwhelming and a runaway mutation process will destroy the information in subsequent generations of the molecule. The error threshold is also controlled by the fitness landscape for the molecules. Molecules that differ only by a few mutations may be thought of as "close" to each other, while those that differ by many mutations are distant from each other. Molecules that are very fit, and likely to reproduce, have a "high" fitness, those less fit have "low" fitness.

These ideas of proximity and height form the intuitive concept of the "fitness landscape". If a particular sequence and its neighbors have a high fitness, they will form a quasispecies and will be able to support longer sequence lengths than a fit sequence with few fit neighbors, or a less fit neighborhood of sequences. Also, it was noted by Wilke (Wilke 2005) that the error threshold concept does not apply in portions of the landscape where there are lethal mutations, in which the induced mutation yields zero fitness and prohibits the molecule from reproducing.

Eigen's Paradox

Eigen's paradox is one of the most intractable puzzles in the study of the origins of life. It is thought that the error threshold concept described above limits the size of self replicating molecules to perhaps a few hundred digits, yet almost all life on earth requires much longer molecules to encode their genetic information. This problem is handled in living cells by enzymes that repair mutations, allowing the encoding molecules to reach sizes on the order of millions of base pairs. These large molecules must, of course, encode the very enzymes that repair them, and herein lies Eigen's paradox, first put forth by Manfred Eigen in his 1971 paper (Eigen 1971). Simply stated, Eigen's paradox amounts to the following:

This is a chicken-or-egg kind of a paradox, with an even more difficult solution. Which came first, the large genome or the error correction enzymes? A number of solutions to this paradox have been proposed:

A simple mathematical model

Consider a 3-digit molecule [A,B,C] where A, B, and C can take on the values 0 and 1. There are eight such sequences ([000], [001], [010], [011], [100], [101], [110], and [111]). Let's say that the [000] molecule is the most fit; upon each replication it produces an average of a copies, where a > 1 . This molecule is called the "master sequence". The other seven sequences are less fit; they each produce only 1 copy per replication. The replication of each of the three digits is done with a mutation rate of μ. In other words, at every replication of a digit of a sequence, there is a probability μ that it will be erroneous; 0 will be replaced by 1 or vice versa. Let's ignore double mutations and the death of molecules (the population will grow infinitely), and divide the eight molecules into three classes depending on their Hamming distance from the master sequence:

Note that the number of sequences for distance d is just the binomial coefficient ( L d ) for L=3, and that each sequence can be visualized as the vertex of an L=3 dimensional cube, with each edge of the cube specifying a mutation path in which the change Hamming distance is either zero or ±1. It can be seen that, for example, one third of the mutations of the [001] molecules will produce [000] molecules, while the other two thirds will produce the class 2 molecules [011] and [101]. We can now write the expression for the child populations n i ′ of class i in terms of the parent populations n j .

where the fitness matrix w according to quasispecies model is given by:

where Q = ( 1 − μ ) L is the probability that an entire molecule will be replicated successfully. The eigenvectors of the w matrix will yield the equilibrium population numbers for each class. For example, if the mutation rate μ is zero, we will have Q=1, and the equilibrium concentrations will be [ n 0 , n 1 , n 2 , n 3 ] = [ 1 , 0 , 0 , 0 ] . The master sequence, being the fittest will be the only one to survive. If we have a replication fidelity of Q=0.95 and genetic advantage of a=1.05, then the equilibrium concentrations will be roughly [ 0.33 , 0.38 , 0.24 , 0.06 ] . It can be seen that the master sequence is not as dominant, however, sequences with low Hamming distance are in majority. If we have a replication fidelity of Q approaching 0, then the equilibrium concentrations will be roughly [ 0.125 , 0.375 , 0.375 , 0.125 ] . This is a population with equal number of each of 8 sequences. (If we had perfectly equal population of all sequences, we would have populations of [1,3,3,1]/8.)

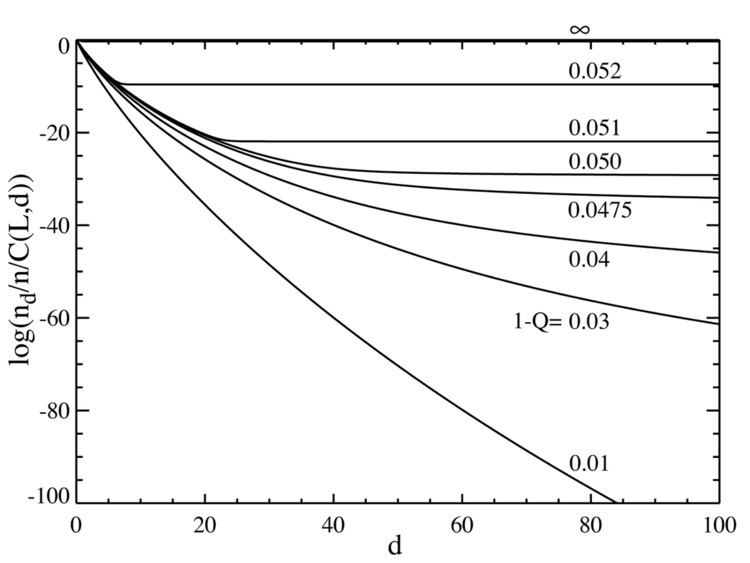
If we now go to the case where the number of base pairs is large, say L=100, we obtain behavior that resembles a phase transition. The plot below on the left shows a series of equilibrium concentrations divided by the binomial coefficient ( 100 k ) . (This multiplication will show the population for an individual sequence at that distance, and will yield a flat line for an equal distribution.) The selective advantage of the master sequence is set at a=1.05. The horizontal axis is the Hamming distance d . The various curves are for various total mutation rates ( 1 − Q ) . It is seen that for low values of the total mutation rate, the population consists of a quasispecies gathered in the neighborhood of the master sequence. Above a total mutation rate of about 1-Q=0.05, the distribution quickly spreads out to populate all sequences equally. The plot below on the right shows the fractional population of the master sequence as a function of the total mutation rate. Again it is seen that below a critical mutation rate of about 1-Q=0.05, the master sequence contains most of the population, while above this rate, it contains only about 2 − L ≈ 10 − 30 of the total population.

It can be seen that there is a sharp transition at a value of 1-Q  just a bit larger than 0.05. For mutation rates above this value, the population of the master sequence drops to practically zero. Above this value, it dominates.

In the limit as L approaches infinity, the system does in fact have a phase transition at a critical value of Q: Q c = 1 / a . . One could think of the overall mutation rate (1-Q) as a sort of "temperature", which "melts" the fidelity of the molecular sequences above the critical "temperature" of 1 − Q c . For faithful replication to occur, the information must be "frozen" into the genome.