Vertices 12 Symmetry group D5h, [5,2], (*522) | Edges 25 Vertex configuration 10(3.4)2(3) | |
 | ||
Type JohnsonJ15 - J16 - J17 | ||
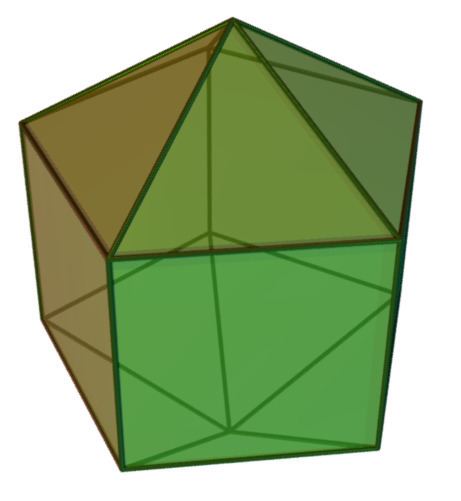
In geometry, the elongated pentagonal bipyramid is one of the Johnson solids (J16). As the name suggests, it can be constructed by elongating a pentagonal bipyramid (J13) by inserting a pentagonal prism between its congruent halves.
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
Dual polyhedron
The dual of the elongated square bipyramid is a pentagonal bifrustum.
References
Elongated pentagonal bipyramid Wikipedia(Text) CC BY-SA
