Elastic instability

Single degree of freedom-systems

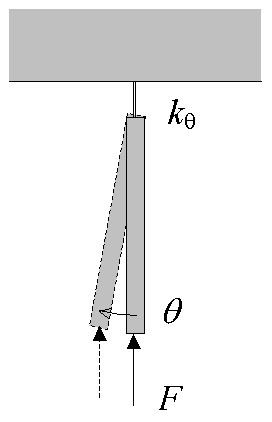
Consider as a simple example a rigid beam of length L, hinged in one end and free in the other, and having an angular spring attached to the hinged end. The beam is loaded in the free end by a force F acting in the compressive axial direction of the beam, see the figure to the right.

Moment equilibrium condition

Assuming a clockwise angular deflection θ , the clockwise moment exerted by the force becomes M F = F L sin ⁡ θ . The moment equilibrium equation is given by

F L sin ⁡ θ = k θ θ

where k θ is the spring constant of the angular spring (Nm/radian). Assuming θ is small enough, implementing the Taylor expansion of the sine function and keeping the two first terms yields

F L ( θ − 1 6 θ 3 ) ≈ k θ θ

which has three solutions, the trivial θ = 0 , and

θ ≈ ± 6 ( 1 − k θ F L )

which is imaginary (i.e. not physical) for F L < k θ and real otherwise. This implies that for small compressive forces, the only equilibrium state is given by θ = 0 , while if the force exceeds the value k θ / L there is suddenly another mode of deformation possible.

Energy method

The same result can be obtained by considering energy relations. The energy stored in the angular spring is

E s p r i n g = ∫ k θ θ d θ = 1 2 k θ θ 2

and the work done by the force is simply the force multiplied by the vertical displacement of the beam end, which is L ( 1 − cos ⁡ θ ) . Thus,

E f o r c e = ∫ F d x = F L ( 1 − cos ⁡ θ )

The energy equilibrium condition E s p r i n g = E f o r c e now yields F = k θ / L as before (besides from the trivial θ = 0 ).

Stability of the solutions

Any solution θ is stable iff a small change in the deformation angle Δ θ results in a reaction moment trying to restore the original angle of deformation. The net clockwise moment acting on the beam is

M ( θ ) = F L sin ⁡ θ − k θ θ

An infinitesimal clockwise change of the deformation angle θ results in a moment

M ( θ + Δ θ ) = M + Δ M = F L ( sin ⁡ θ + Δ θ cos ⁡ θ ) − k θ ( θ + Δ θ )

which can be rewritten as

Δ M = Δ θ ( F L cos ⁡ θ − k θ )

since F L sin ⁡ θ = k θ θ due to the moment equilibrium condition. Now, a solution θ is stable iff a clockwise change Δ θ > 0 results in a negative change of moment Δ M < 0 and vice versa. Thus, the condition for stability becomes

Δ M Δ θ = d M d θ = F L cos ⁡ θ − k θ < 0

The solution θ = 0 is stable only for F L < k θ , which is expected. By expanding the cosine term in the equation, the approximate stability condition is obtained:

| θ | > 2 ( 1 − k θ F L )

for F L > k θ , which the two other solutions satisfy. Hence, these solutions are stable.

Multiple degrees of freedom-systems

By attaching another rigid beam to the original system by means of an angular spring a two degrees of freedom-system is obtained. Assume for simplicity that the beam lengths and angular springs are equal. The equilibrium conditions become

F L ( sin ⁡ θ 1 + sin ⁡ θ 2 ) = k θ θ 1

F L sin ⁡ θ 2 = k θ ( θ 2 − θ 1 )

where θ 1 and θ 2 are the angles of the two beams. Linearizing by assuming these angles are small yields

( F L − k θ F L k θ F L − k θ ) ( θ 1 θ 2 ) = ( 0 0 )

The non-trivial solutions to the system is obtained by finding the roots of the determinant of the system matrix, i.e. for

F L k θ = 3 2 ∓ 5 2 ≈ { 0.382 2.618

Thus, for the two degrees of freedom-system there are two critical values for the applied force F. These correspond to two different modes of deformation which can be computed from the nullspace of the system matrix. Dividing the equations by θ 1 yields

θ 2 θ 1 | θ 1 ≠ 0 = k θ F L − 1 ≈ { 1.618 for  F L / k θ ≈ 0.382 − 0.618 for  F L / k θ ≈ 2.618

For the lower critical force the ratio is positive and the two beams deflect in the same direction while for the higher force they form a "banana" shape. These two states of deformation represent the buckling mode shapes of the system.