Eight vertex model

Description

As with the ice-type models, the eight-vertex model is a square lattice model, where each state is a configuration of arrows at a vertex. The allowed vertices have an even number of arrows pointing towards the vertex; these include the six inherited from the ice-type model (1-6), and sinks and sources (7, 8).

We consider a N × N lattice, with N 2 vertices and 2 N 2 edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex j has an associated energy ϵ j and Boltzmann weight w j = e − ϵ j k T , giving the partition function over the lattice as

where the summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.

Solution in the zero-field case

The zero-field case of the model corresponds physically to the absence of external electric fields. Hence, the model remains unchanged under the reversal of all arrows; the states 1 and 2, and 3 and 4, consequently must occur as pairs. The vertices can be assigned arbitrary weights

The solution is based on the observation that rows in transfer matrices commute, for a certain parametrisation of these four Boltzmann weights. This came about as a modification of an alternate solution for the six-vertex model; it makes use of elliptic theta functions.

Commuting transfer matrices

The proof relies on the fact that when Δ ′ = Δ and Γ ′ = Γ , for quantities

the transfer matrices T and T ′ (associated with the weights a , b , c , d and a ′ , b ′ , c ′ , d ′ ) commute. Using the star-triangle relation, Baxter reformulated this condition as equivalent to a parametrisation of the weights given as

for fixed modulus k and η and variable u . Here snh is the hyperbolic analogue of sn, given by

and H ( u ) and Θ ( u ) are Jacobi elliptic functions of modulus k . The associated transfer matrix T thus is a function of u alone; for all u , v

The matrix function Q ( u ) {displaystyle Q(u)}

The other crucial part of the solution is the existence of a nonsingular matrix-valued function Q , such that for all complex u the matrices Q ( u ) , Q ( u ′ ) commute with each other and the transfer matrices, and satisfy

where

The existence and commutation relations of such a function are demonstrated by considering pair propagations through a vertex, and periodicity relations of the theta functions, in a similar way to the six-vertex model.

Explicit solution

The commutation of matrices in (1) allow them to be diagonalised, and thus eigenvalues can be found. The partition function is calculated from the maximal eigenvalue, resulting in a free energy per site of

for

where K and K ′ are the complete elliptic integrals of moduli k and k ′ . The eight vertex model was also solved in quasicrystals.

Equivalence with an Ising model

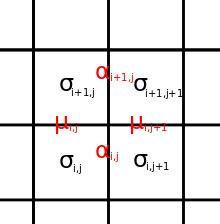
There is a natural correspondence between the eight-vertex model, and the Ising model with 2-spin and 4-spin nearest neighbour interactions. The states of this model are spins σ = ± 1 on faces of a square lattice. The analogue of 'edges' in the eight-vertex model are products of spins on adjacent faces:

The most general form of the energy for this model is

where J h , J v , J , J ′ describe the horizontal, vertical and two diagonal 2-spin interactions, and J ″ describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.

We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model μ , α respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising 'edges'. Each σ configuration then corresponds to a unique μ , α configuration, whereas each μ , α configuration gives two choices of σ configurations.

Equating general forms of Boltzmann weights for each vertex j , the following relations between the ϵ j and J h , J v , J , J ′ , J ″ define the correspondence between the lattice models:

It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.

These relations gives the equivalence Z I = 2 Z 8 V between the partition functions of the eight-vertex model, and the 2,4-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.