Effect Model law - Alchetron, The Free Social Encyclopedia

The Effect Model law states that a natural relationship exists for each individual between the frequency (observation) or the probability (prediction) of a morbid event without any treatment ( R c ) and the frequency or probability of the same event with a treatment ( R t ) . This relationship applies to a single individual, individuals within a population, or groups. This law enables the prediction of the (absolute) benefit ( A B ) of a treatment for a given patient. It has wide-reaching implications in R&D for new pharmaceutical products as well as personalized medicine. The law was serendipitously discovered in the 1990s by Jean-Pierre Boissel. While studying the effectiveness of class-I antiarrhythmic drugs in the prevention of death after myocardial infarction, he stumbled upon a situation which contradicts one of the basic premises of meta-analysis theory, i.e. that the heterogeneity test was significant at the same time for the assumption “the relative risk ( R R ) is a constant” and “ A B is a constant”.

Boissel formulated the hypothesis that the antiarrhythmic drugs efficacy was a function combining a beneficial effect ( a ) that is proportional to R c and a constant adverse effect ( b ), independent of R c . The mathematical expression of this model is a linear equation with two parameters, the risk of lethal adverse event caused by treatment and the slope of the line which represents the true beneficial risk reduction. This equation gives the treatment net mortality reduction: R t = a × R c + b

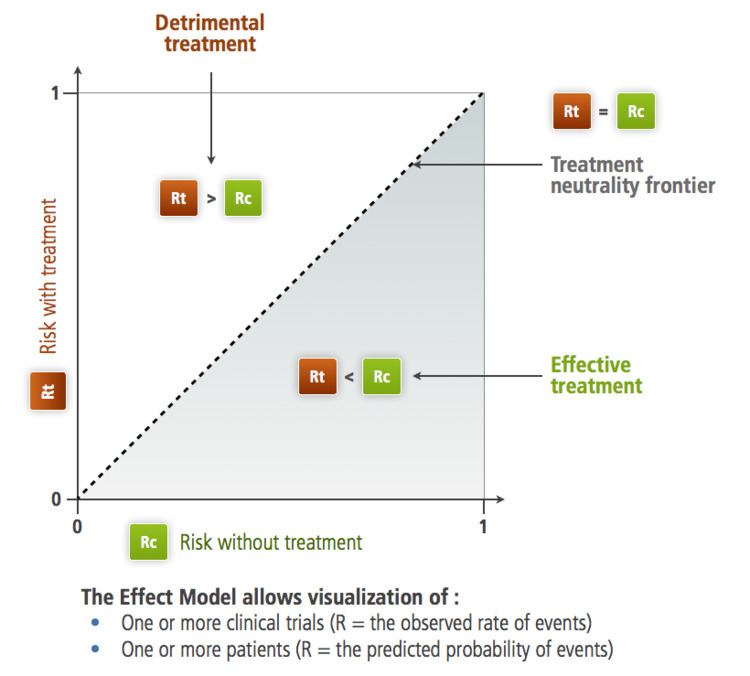
Illustration in the (Rc,Rt) plane

In 1987, L'Abbe, Detsky and O'Rourke recommended including a graphical representation of the various trials while designing a meta-analysis. For each trial, on the x-axis the frequency (risk) of the studied criterion in the control group ( R c ) should be represented, and on the y-axis, the risk in the treated group ( R t ) (Figure 1 and Figure 2).

The shape of the resulting scatter plot illustrates some important aspects of the information concerning the effect of the treatment:

On an individual basis, the ability to measure and predict the absolute benefit of a treatment for a patient characterized by his or her idiosyncratic risk parameters (e.g., cholesterol level, systolic blood pressure, etc.);

Over a given population (e.g., French, Chinese, etc.), the ability to measure and predict health outcomes for a treatment available on the market or a drug candidate at any stage in the R&D process (from the target identification phase to clinical trials).

The law is expressed in two ways.

the R t function: R t = f ( R c , X ) or R t = g ( Y , X ) , equation in which R c is implicit.
the absolute benefit function A B : A B = R c − R t = h ( Y , X ) , equation in which R t and R c are implicit.

The forms above lead to as many values in the ( R c , R t ) plane as there are patients, each one being represented by a dot which is more or less close to the neutrality frontier. The expression of the absolute benefit A B (i.e. the vertical distance to the neutrality frontier) has the advantage of leading directly to an individual prediction, making personalized medicine a practical reality. The X and Y are, respectively, patients descriptors linked with R c and with the treatment × patient interactions.

By summing up A B i over the entire population of interest, the model yields a quantified efficacy metric over “real” patients, called the Number of Prevented Events (NPE). Since each patient responds to a proposed therapy in a different way, it is too simplistic to consider a digital outcome for a treatment, i.e. efficient or inefficient. Rather, a given patient will benefit by an order of magnitude which will vary depending on his or her risk profile. This magnitude is measured by the quantity:

This illustrates an intuition that all doctors have, and that Kaurer and Kassirer emphasized in 1980: a treatment can yield little benefit; even worse, it can be more harmful than beneficial for "moderately sick" patients. In the case where the Effect Model is curvilinear, as shown in Figure 2, it is easy to understand intuitively that:

Low-risk patients (e.g. R c < 0.1 ) don’t benefit from the treatment as much as higher-risk patients;

High-risk patients (e.g. R c > 0.9 ) are less likely to avoid the clinical event, irrespective of the treatment.

Evidence of the existence of the law

Evidence of the existence of the Effect Model law is supported by empirical observations (the aforementioned study of antiarrhythmic drugs in post-myocardial infarction), simulations as well as a theoretical demonstration. The simulation approach consists in combining a mathematical model of the disease of interest and the intended treatment, combining it with a population of virtual patients and in applying the disease model and then the therapeutic model (treatment acting on the disease) to every virtual subject. The outcome is always a connection between R t and R c (refer to Figure 3 below).

A proof of the intrinsic nature of the Effect Model is that it emerges from the combination of a disease model and a virtual population without being explicitly accounted for in the modeling process.

Applications: bridging the efficacy-effectiveness gap

In a 2011 Nature article, authors showed that it is necessary to develop and use a broad range of methods to be able to bridge the efficacy-effectiveness gap frequently observed in clinical practice. This gap stems from the differences between satisfactory efficacy data from clinical trials and the actual health outcomes observed in real life once the drug enters the market. In this context, the NPE can serve as a decision-support metric to drive resources allocation across a pipeline of pharmaceutical products, conduct comparative effectiveness analyses versus standard of care and cost-effectiveness studies. All of these combine into a powerful framework to establish the proof of commercial relevance of a drug product to regulators and payers in the context of pricing & reimbursement negotiations.

It is expected that the Effect Model will gradually emerge as an industry standard accepted by regulatory and paying agencies to support their decisions. A first milestone was reached in February 2013 with the publication of a guideline by the European Network for Health Technology Assessment (eunethta) on the Relative Assessment of Pharmaceuticals, which mentions the Effect Model.

Transposability

There are 2 dimensions to transposability studies:

The way clinical trial results – arguably an idealized setting, “transpose” into real-life patient outcomes on a selected population;

In turn, how these results “transpose” from one population to another.

The Effect Model enables the simulation of a drug candidate’s impact on real populations. It also provides a powerful framework to explore the drivers of transposability of clinical trials results for a same drug from one population to another.

Comparative effectiveness

With the payer-driven market’s shift from buying drug products to buying patient outcomes – as a result of mounting fiscal imbalances, proof of concept is not sufficient anymore. Pharmaceutical companies must establish the proof of commercial relevance, or superiority of their product over the standard of care. With that in mind, the Effect Model is used to:

Continuously benchmark a drug candidate’s value, as it progresses from discovery to clinical development, versus the prevailing comparator;

Identify and characterize subgroups of patients where the drug candidate shows superior efficacy, if and when traditional clinical trials fail to demonstrate, on average, superior value.

Cost effectiveness

The proof of commercial value should explicitly incorporate pricing considerations. What is being calculated in this instance is the Cost per Prevented Event. Given:

The total amount of spending earmarked by a social security system to treat a particular disease;

The treatment’s proposed unit price;

One can derive:

The number of individuals who can be treated and the associated A B i threshold;

The Cost per Prevented Event.

R&D decision support

The Effect Model and its associated concept of NPE provide an invaluable framework to base resources allocation decisions on an unbiased and informed representation of the predicted health outcomes of the product under development. A large number of hypotheses can be tested against this NPE metric, from early discovery to clinical development and market access. Examples include:

The identification of optimal therapeutic targets included in the disease model;

The identification of the optimal vector of theranostic biomarkers;

The characterization of optimal patient responders to reduce the size of clinical trials without negatively impacting the statistical significance of results.

Personalized medicine

Given a patient’s idiosyncratic risk factor values (e.g. cholesterol level, systolic blood pressure, etc.) and other patient descriptors linked with treatment efficacy (i.e. X and Y ), it is possible to locate him or her in the ( R c , R t ) plane and estimate the associated A B i between competing treatments. In this instance, the Effect Model serves as a powerful framework to support prescription decisions in day-to-day medical practice.

Number Needed to Treat (NNT) and Number of Prevented Events (NPE)

The Number Needed to Treat (NNT) is often used to benchmark medicines. The drug with the lowest NNT is said to be more efficient than its competitors. However, the NNT benchmark is fundamentally flawed in its construct. NNT varies with treatment and/or follow-up duration, as shown by Kassaï et al. and Kristiansen and Gyrd-Hansen. It is therefore impossible to make apples-to-apples comparative analyses with this benchmark. For instance, there is no constant follow-up duration across diverse treatments’ randomized clinical trials that are used to compute the NNT.

A more fundamental weakness is the fact that the NNT changes with each patient’s profile. And there are large differences in average patient Rc, a profile marker, between trials in a given domain.

With the Effect Model law and the associated Number of Prevented Events (NPE), it becomes possible to account for this patient profile variability in a structured and cohesive way, thus enabling apples-to-apples benchmarking.

The NNT fallacy has been denounced by several authors since Cook and Sackett, who cautioned that the NNT should not be used in patients with different baseline risks without a correction in the particular context of personalized medical decision. However, the correction these authors suggested does work only if the treatment’s absolute benefit is a linear function of the baseline risk, as for the beta-blocker case, which is not always true as shown when the Effect Model is curvilinear.

References

Effect Model law Wikipedia

(Text) CC BY-SA

Contents