 | ||
If a fluid is not moving, the measured pressure is the same in all directions static pressure. But if the fluid is moving, the measured pressure depends both on the Static pressure and on the pressure caused by the energy of its motion, in the direction of that motion. The added pressure from the fluid's motion is called dynamic pressure. In incompressible fluid dynamics dynamic pressure (indicated with q, or Q, and sometimes called velocity pressure) is the quantity defined by:
Contents
where (using SI units):
Physical meaning
Dynamic pressure is the kinetic energy per unit volume of a fluid particle. Dynamic pressure is in fact one of the terms of Bernoulli's equation, which can be derived from the conservation of energy for a fluid in motion. In simplified cases, the dynamic pressure is equal to the difference between the stagnation pressure and the static pressure.
Another important aspect of dynamic pressure is that, as dimensional analysis shows, the aerodynamic stress (i.e. stress within a structure subject to aerodynamic forces) experienced by an aircraft travelling at speed
Uses
The dynamic pressure, along with the static pressure and the pressure due to elevation, is used in Bernoulli's principle as an energy balance on a closed system. The three terms are used to define the state of a closed system of an incompressible, constant-density fluid.
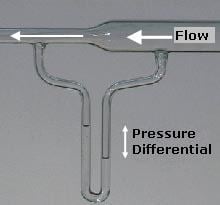
If we were to divide the dynamic pressure by the product of fluid density and acceleration due to gravity, g, the result is called velocity head, which is used in head equations like the one used for pressure head and hydraulic head. In a venturi flow meter, the differential pressure head can be used to calculate the differential velocity head, which are equivalent in the adjacent picture. An alternative to velocity head is dynamic head.
Compressible flow
Many authors define dynamic pressure only for incompressible flows. (For compressible flows, these authors use the concept of impact pressure.) However, the definition of dynamic pressure can be extended to include compressible flows.
If the fluid in question can be considered an ideal gas (which is generally the case for air), the dynamic pressure can be expressed as a function of fluid pressure and Mach number.
By applying the ideal gas law:
the definition of the speed of sound
and also
where (using SI units):
