 | ||
Dynamic epistemic logic
Dynamic epistemic logic (DEL) is a logical framework dealing with knowledge and information change. Typically, DEL focuses on situations involving multiple agents and studies how their knowledge changes when events occur. These events can change factual properties of the actual world (they are called ontic events): for example a red card is painted in blue. They can also bring about changes of knowledge without changing factual properties of the world (they are called epistemic events): for example a card is revealed publicly (or privately) to be red. Originally, DEL focused on epistemic events. We only present in this entry some of the basic ideas of the original DEL framework; more details about DEL in general can be found in the references.
Contents
- Dynamic epistemic logic
- Epistemic Logic
- Syntax
- Semantics
- Knowledge versus Belief
- Axiomatization
- Decidability and Complexity
- Adding Dynamics
- Public Events
- Arbitrary Events
- Event Model
- Product Update
- References
Due to the nature of its object of study and its abstract approach, DEL is related and has applications to numerous research areas, such as computer science (artificial intelligence), philosophy (formal epistemology), economics (game theory) and cognitive science. In computer science, DEL is for example very much related to multi-agent systems, which are systems where multiple intelligent agents interact and exchange information.
As a combination of dynamic logic and epistemic logic, dynamic epistemic logic is a young field of research. It really started in 1989 with Plaza’s logic of public announcement. Independently, Gerbrandy and Groeneveld proposed a system dealing moreover with private announcement and that was inspired by the work of Veltman. Another system was proposed by van Ditmarsch whose main inspiration was the Cluedo game. But the most influential and original system was the system proposed by Baltag, Moss and Solecki. This system can deal with all the types of situations studied in the works above and its underlying methodology is conceptually grounded. We will present in this entry some of its basic ideas.
Formally, DEL extends ordinary epistemic logic by the inclusion of event models to describe actions, and a product update operator that defines how epistemic models are updated as the consequence of executing actions described through event models. Epistemic logic will first be recalled. Then, actions and events will enter into the picture and we will introduce the DEL framework.
Epistemic Logic
Epistemic logic is a modal logic dealing with the notions of knowledge and belief. As a logic, it is concerned with understanding the process of reasoning about knowledge and belief: which principles relating the notions of knowledge and belief are intuitively plausible? Like epistemology, it stems from the Greek word
Syntax
In the sequel,
The epistemic language is an extension of the basic multi-modal language of modal logic with a common knowledge operator
where
Group notions: general, common and distributed knowledge.
In a multi-agent setting there are three important epistemic concepts: general knowledge, distributed knowledge and common knowledge. The notion of common knowledge was first studied by Lewis in the context of conventions. It was then applied to distributed systems and to game theory, where it allows to express that the rationality of the players, the rules of the game and the set of players are commonly known.
General knowledge.
General knowledge of
Common knowledge.
Common knowledge of
As we do not allow infinite conjunction the notion of common knowledge will have to be introduced as a primitive in our language.
Before defining the language with this new operator, we are going to give an example introduced by Lewis that illustrates the difference between the notions of general knowledge and common knowledge. Lewis wanted to know what kind of knowledge is needed so that the statement
Distributed knowledge.
Distributed knowledge of
Semantics
Epistemic logic is a modal logic. So, what we call an epistemic model
Intuitively, a pointed epistemic model
For every epistemic model
where
Despite the fact that the notion of common belief has to be introduced as a primitive in the language, we can notice that the definition of epistemic models does not have to be modified in order to give truth value to the common knowledge and distributed knowledge operators.
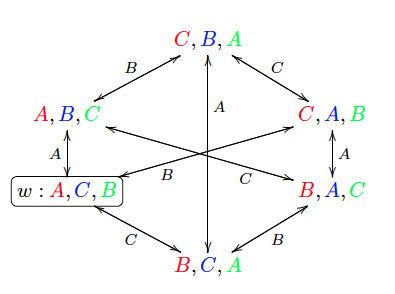
Card Example:
Players
and so on...
When accessibility relations are equivalence relations (like in this example) and we have that
In particular, the following statements hold:
'All the agents know the color of their card'.
'
'Everybody knows that
Knowledge versus Belief
We use the same notation
The notion of knowledge might comply to some other constraints (or axioms) such as
We discuss the axioms above. Axiom 4 states that if the agent knows a proposition, then she knows that she knows it (this axiom is also known as the “KK-principle”or “KK-thesis”). In epistemology, axiom 4 tends to be accepted by internalists, but not by externalists. Axiom 4 is nevertheless widely accepted by computer scientists (but also by many philosophers, including Plato, Aristotle, Saint Augustine, Spinoza and Shopenhauer, as Hintikka recalls ). A more controversial axiom for the logic of knowledge is axiom 5 for Euclidicity: this axiom states that if the agent does not know a proposition, then she knows that she does not know it. Most philosophers (including Hintikka) have attacked this axiom, since numerous examples from everyday life seem to invalidate it. In general, axiom 5 is invalidated when the agent has mistaken beliefs, which can be due for example to misperceptions, lies or other forms of deception. Axiom B states that it cannot be the case that the agent considers it possible that she knows a false proposition (that is,
Axiomatization
The Hilbert proof system K for the basic modal logic is defined by the following axioms and inference rules: for all
The axioms of an epistemic logic obviously display the way the agents reason. For example, the axiom K together with the rule of inference Nec entail that if I know
We define the set of proof systems
Moreover, for all
The relative strength of the proof systems for knowledge is as follows:
So, all the theorems of
For all
Decidability and Complexity
The satisfiability problem for all the logics introduced is decidable. We list below the computational complexity of the satisfiability problem for each of them. Note that it becomes linear in time if there are only finitely many propositional letters in the language. For
The computational complexity of the model checking problem is in P in all cases.
Adding Dynamics
Dynamic Epistemic Logic (DEL) is a logical framework for modeling epistemic situations involving several agents, and changes that occur to these situations as a result of incoming information or more generally incoming action. The methodology of DEL is such that it splits the task of representing the agents’ beliefs and knowledge into three parts:
- One represents their beliefs about an initial situation thanks to an epistemic model;
- One represents their beliefs about an event taking place in this situation thanks to an event model;
- One represents the way the agents update their beliefs about the situation after (or during) the occurrence of the event thanks to a product update.
Typically, an informative event can be a public announcement to all the agents of a formula
Public Events
In this section, we assume that all events are public. We start by giving a concrete example where DEL can be used, to better understand what is going on. This example is called the muddy children puzzle. Then, we will present a formalization of this puzzle in a logic called Public Announcement Logic (PAL). The muddy children puzzle is one of the most well known puzzles that played a role in the development of DEL. Other significant puzzles include the sum and product puzzle, the Monty Hall dilemma, the Russian cards problem, the two envelopes problem, Moore's paradox, the hangman paradox, etc.
Muddy Children Example:
We have two children, A and B, both dirty. A can see B but not himself, and B can see A but not herself. Let
- We represent the initial situation by the pointed epistemic model
( N , s ) represented below, where relations between worlds are equivalence relations. Statess , t , u , v intuitively represent possible worlds, a proposition (for examplep ) satisfiable at one of these worlds intuitively means that in the corresponding possible world, the intuitive interpretation ofp (A is dirty) is true. The links between worlds labelled by agents (A or B) intuitively express a notion of indistinguishability for the agent at stake between two possible worlds. For example, the link betweens andt labelled by A intuitively means that A can not distinguish the possible worlds fromt and vice versa. Indeed, A cannot see himself, so he cannot distinguish between a world where he is dirty and one where he is not dirty. However, he can distinguish between worlds where B is dirty or not because he can see B. With this intuitive interpretation we are brought to assume that our relations between worlds are equivalence relations. - Now, suppose that their father comes and announces that at least one is dirty (formally,
p ∨ q ). Then we update the model and this yields the pointed epistemic model represented below. What we actually do is suppressing the worlds where the content of the announcement is not fulfilled. In our case this is the world where¬ p and¬ q are true. This suppression is what we call the update. We then get the model depicted below. As a result of the announcement, both A and B do know that at least one of them is dirty. We can read this from the epistemic model. - Now suppose there is a second (and final) announcement that says that neither knows they are dirty (an announcement can express facts about the situation as well as epistemic facts about the knowledge held by the agents). We then update similarly the model by suppressing the worlds which do not satisfy the content of the announcement, or equivalently by keeping the worlds which do satisfy the announcement. This update process thus yields the pointed epistemic model represented below. By interpreting this model, we get that A and B both know that they are dirty, which seems to contradict the content of the announcement. However, if we assume that A and B are both perfect reasoners and that this is common knowledge among them, then this inference makes perfect sense.
Public announcement logic (PAL):
We present the syntax and semantic of Public Announcement Logic (PAL), which combines features of epistemic logic and propositional dynamic logic.
We define the language
where
The language
where
The formula
The proof system
The axioms Red 1 - Red 4 are called reduction axioms because they allow to reduce any formula of
PAL is decidable, its model checking problem is solvable in polynomial time and its satisfiability problem is PSPACE-complete.
Muddy children puzzle formalized with PAL:
Here are some of the statements that hold in the muddy children puzzle formalized in PAL.
'In the initial situation, A is dirty and B is dirty'.
'In the initial situation, A does not know whether he is dirty and B neither'.
'After the public announcement that at least one of the children A and B is dirty, both of then know that at least one of them is dirty'. However:
'After the public announcement that at least one of the children A and B is dirty, they still do not know that they are dirty'. Moreover:
'After the successive public announcements that at least one of the children A and B is dirty and that they still do not know whether they are dirty, A and B then both know that they are dirty'.
In this last statement, we see at work an interesting feature of the update process: a formula is not necessarily true after being announced. That is what we technically call “self-persistence” and this problem arises for epistemic formulas (unlike propositional formulas). One must not confuse the announcement and the update induced by this announcement, which might cancel some of the information encoded in the announcement.
Arbitrary Events
In this section, we assume that events are not necessarily public and we focus on items 2 and 3 above, namely on how to represent events and on how to update an epistemic model with such a representation of events by means of a product update.
Event Model
Epistemic models are used to model how agents perceive the actual world. Their perception can also be described in terms of knowledge and beliefs about the world and about the other agents’ beliefs. The insight of the DEL approach is that one can describe how an event is perceived by the agents in a very similar way. Indeed, the agents’ perception of an event can also be described in terms of knowledge and beliefs. For example, the private announcement of
A pointed event model
An event model is a tuple
Card Example:
Let us resume the card example and assume that players
The possible event
Another example of event model is given below. This second example corresponds to the event whereby Player
Product Update
The DEL product update is defined below. This update yields a new pointed epistemic model
Let
If
Card Example:
As a result of the first event described above (Players
The result of the second event is represented below. In this pointed epistemic model, the following statement holds:
Based on these three components (epistemic model, event model and product update), Baltag, Moss and Solecki defined a general logical language inspired from the logical language of propositional dynamic logic to reason about information and knowledge change.
