In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of square brackets [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of brackets, such as arithmetic or algebraic expressions. It is named after the mathematician Walther von Dyck.
Let
Σ
=
{
[
,
]
}
be the alphabet consisting of the symbols [ and ] and let
Σ
∗
denote its Kleene closure. For any element
u
∈
Σ
∗
with length
|
u
|
we define partial functions
i
n
s
e
r
t
:
Σ
∗
×
N
∪
{
0
}
→
Σ
∗
and
d
e
l
e
t
e
:
Σ
∗
×
N
→
Σ
∗
by
i
n
s
e
r
t
(
u
,
j
)
is
u
with "
[
]
" inserted into the
j
th position
d
e
l
e
t
e
(
u
,
j
)
is
u
with "
[
]
" deleted from the
j
th position
with the understanding that
i
n
s
e
r
t
(
u
,
j
)
is undefined for
j
>
|
u
|
and
d
e
l
e
t
e
(
u
,
j
)
is undefined if
j
>
|
u
|
−
2
. We define an equivalence relation
R
on
Σ
∗
as follows: for elements
a
,
b
∈
Σ
∗
we have
(
a
,
b
)
∈
R
if and only if there exists a finite sequence of applications of the
i
n
s
e
r
t
and
d
e
l
e
t
e
functions starting with
a
and ending with
b
, where the empty sequence is allowed. That the empty sequence is allowed accounts for the reflexivity of
R
. Symmetry follows from the observation that any finite sequence of applications of
i
n
s
e
r
t
to a string can be undone with a finite sequence of applications of
d
e
l
e
t
e
. Transitivity is clear from the definition.
The equivalence relation partitions the language
Σ
∗
into equivalence classes. If we take
ϵ
to denote the empty string, then the language corresponding to the equivalence class
Cl
(
ϵ
)
is called the Dyck language.
An alternative definition of the Dyck language can be formulated when we introduce the
i
m
b
a
l
a
n
c
e
:
Σ
∗
→
(
N
∪
{
0
}
)
function.
i
m
b
a
l
a
n
c
e
(
u
)
=
|
u
|
[
−
|
u
|
]
for any
u
∈
Σ
∗
.
where
|
u
|
[
and
|
u
|
]
are respectively the number of [ and ] in
u
. I.e.
i
m
b
a
l
a
n
c
e
counts the imbalance of [ over ]. If
i
m
b
a
l
a
n
c
e
(
u
)
is positive then
u
has more [ than ].
Now, the Dyck language can be defined as the language
{
u
∈
Σ
∗
|
i
m
b
a
l
a
n
c
e
(
u
)
=
0
and
i
m
b
a
l
a
n
c
e
(
v
)
≥
0
for all prefixes
v
of
u
}
The Dyck language is closed under the operation of concatenation.
By treating
Σ
∗
as an algebraic monoid under concatenation we see that the monoid structure transfers onto the quotient
Σ
∗
/
R
, resulting in the syntactic monoid of the Dyck language. The class
Cl
(
ϵ
)
will be denoted
1
.
The syntactic monoid of the Dyck language is not commutative: if
u
=
Cl
(
[
)
and
v
=
Cl
(
]
)
then
u
v
=
Cl
(
[
]
)
=
1
≠
Cl
(
]
[
)
=
v
u
.
With the notation above,
u
v
=
1
but neither
u
nor
v
are invertible in
Σ
∗
/
R
.
The syntactic monoid of the Dyck language is isomorphic to the bicyclic semigroup by virtue of the properties of
Cl
(
[
)
and
Cl
(
]
)
described above.
By the Chomsky–Schützenberger representation theorem, any context-free language is a homomorphic image of the intersection of some regular language with a homomorphic preimage of the Dyck language on two brackets.
The Dyck language with two distinct types of brackets can be recognized in the complexity class
T
C
0
.
We can define an equivalence relation
L
on the Dyck language
D
. For
u
,
v
∈
D
we have
(
u
,
v
)
∈
L
if and only if
|
u
|
=
|
v
|
, i.e.
u
and
v
have the same length. This relation partitions the Dyck language
D
/
L
=
D
0
∪
D
2
∪
D
4
∪
…
=
⋃
n
=
0
∞
D
n
where
D
n
=
{
u
∈
D
∣
|
u
|
=
n
}
. Note that
D
n
is empty for odd
n
. E.g. there are 14 words in
D
8
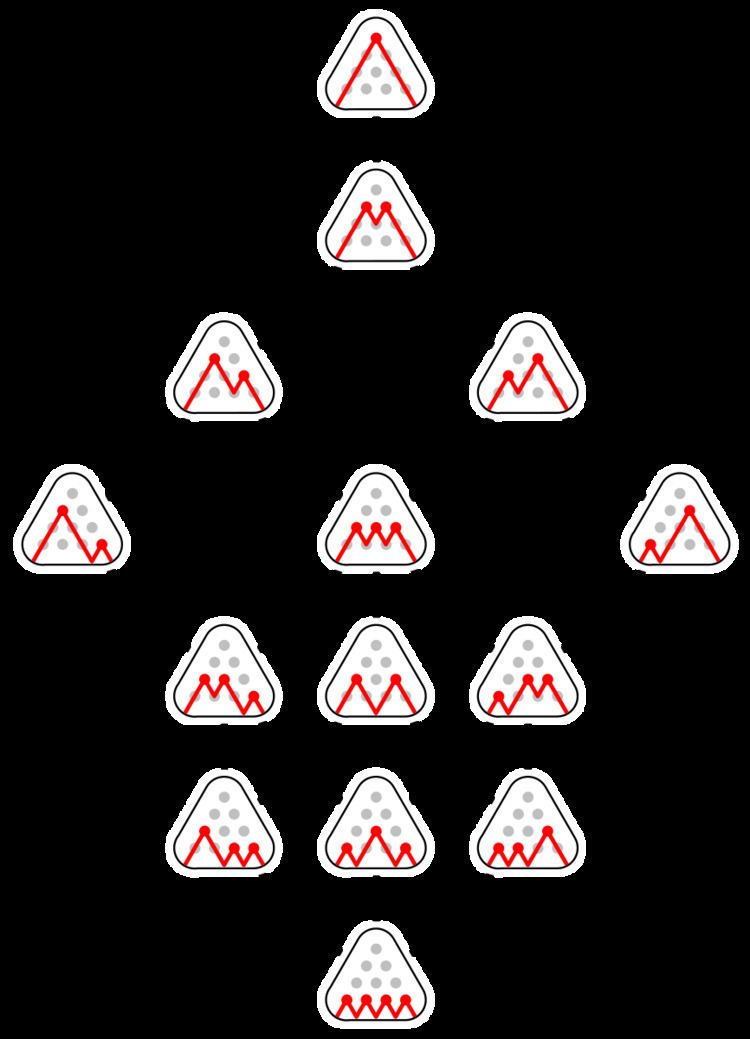
, i.e. [[[[]]]], [[[][]]], [[[]][]], [[][[]]], [[[]]][], [[][][]], [][[[]]], [[][]][], [[]][[]], [][[][]], [[]][][], [][[]][], [][][[]], [][][][].
Having introduced the Dyck words of length
n
, we can introduce a relationship on them. For every
n
∈
N
we define a relation
S
n
on
D
n
; for
u
,
v
∈
D
n
we have
(
u
,
v
)
∈
S
n
if and only if
v
can be reached from
u
by a series of proper swaps. A proper swap in a word
u
∈
D
n
swaps an occurrence of '][' with '[]'. For each
n
∈
N
the relation
S
n
makes
D
n
into a partially ordered set. The relation
S
n
is reflexive because an empty sequence of proper swaps takes
u
to
u
. Transitivity follows because we can extend a sequence of proper swaps that takes
u
to
v
by concatenating it with a sequence of proper swaps that takes
v
to
w
forming a sequence that takes
u
into
w
. To see that
S
n
is also antisymmetric we introduce an auxiliary function
σ
n
:
D
n
→
N
:
u
↦
∑
v
w
=
u
i
m
b
a
l
a
n
c
e
(
v
)
where
v
ranges over all prefixes of
u
. The following table illustrates that
σ
n
is strictly monotonic with respect to proper swaps.
Hence
σ
n
(
u
′
)
−
σ
n
(
u
)
=
2
>
0
so
σ
n
(
u
)
<
σ
n
(
u
′
)
when there is a proper swap that takes
u
into
u
′
. Now if we assume that both
(
u
,
v
)
,
(
v
,
u
)
∈
S
n
and
u
≠
v
, then there are non-empty sequences of proper swaps such
u
is taken into
v
and vice versa. But then
σ
n
(
u
)
<
σ
n
(
v
)
<
σ
n
(
u
)
which is nonsensical. Therefore, whenever both
(
u
,
v
)
and
(
v
,
u
)
are in
S
n
, we have
u
=
v
, hence
S
n
is antisymmetric.
The partial ordered set
D
8
is shown in the illustration accompanying the introduction if we interpret a [ as going up and ] as going down.