 | ||
In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered by (and named after) Charles Dupin in his 1803 dissertation under Gaspard Monge. The key property of a Dupin cyclide is that it is a channel surface (envelope of a one-parameter family of spheres) in two different ways. This property means that Dupin cyclides are natural objects in Lie sphere geometry.
Contents
- Definitions and properties
- Parametric and implicit representation
- Elliptic cyclides
- Parabolic cyclides
- Dupin cyclides and geometric inversions
- Example cylinder
- Example cone
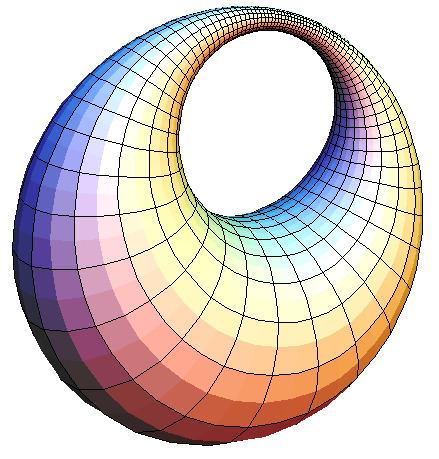
- Example torus
- Separation of variables
- References
Dupin cyclides are often simply known as cyclides, but the latter term is also used to refer to a more general class of quartic surfaces which are important in the theory of separation of variables for the Laplace equation in three dimensions.
Dupin cyclides were investigated not only by Dupin, but also by A. Cayley und J.C. Maxwell.
Today, Dupin cylides are used in computer-aided design (CAD), because cyclide patches have rational representations and are suitable for blending canal surfaces (cylinder, cones, tori, and others).
Definitions and properties
There are several equivalent definitions of Dupin cyclides. In
Since a standard torus is the orbit of a point under a two dimensional abelian subgroup of the Möbius group, it follows that the cyclides also are, and this provides a second way to define them.
A third property which characterizes Dupin cyclides is that their curvature lines are all circles (possibly through the point at infinity). Equivalently, the curvature spheres, which are the spheres tangent to the surface with radii equal to the reciprocals of the principal curvatures at the point of tangency, are constant along the corresponding curvature lines: they are the tangent spheres containing the corresponding curvature lines as great circles. Equivalently again, both sheets of the focal surface degenerate to conics. It follows that any Dupin cyclide is a channel surface (i.e., the envelope of a one-parameter family of spheres) in two different ways, and this gives another characterization.
The definition in terms of spheres shows that the class of Dupin cyclides is invariant under the larger group of all Lie sphere transformations; any two Dupin cyclides are Lie-equivalent. They form (in some sense) the simplest class of Lie-invariant surfaces after the spheres, and are therefore particularly significant in Lie sphere geometry.
The definition also means that a Dupin cyclide is the envelope of the one-parameter family of spheres tangent to three given mutually tangent spheres. It follows that it is tangent to infinitely many Soddy's hexlet configurations of spheres.
Parametric and implicit representation
(CS): A Dupin cyclide can be represented in two ways as the envelope of a one parametric pencil of spheres, i.e. it is a canal surface with two directrices. The pair of directrices consists either of an ellipse and a hyperbola or of two parabolas. In the first case one defines the cyclide as elliptic, in the second case as parabolic. In both cases the conics are contained in two mutually orthogonal planes. In extreme cases (if the ellipse is a circle) the hyperbola degenerates to a line and the cyclide is a torus of revolution.A further special property of a cyclide is:
(CL): Any curvature line of a Dupin cyclide is a circle.Elliptic cyclides
An elliptic cyclide can be represented parametrically by the following formulas (s. weblinks):
The numbers
For
The corresponding implicit representation is:
In case of
Parabolic cyclides
A parabolic cyclide can be represented by the following parametric representation:
The number
A corresponding implicit representation is
Remark: By displaying the circles there appear gaps which are caused by the necessary restriction of the parameters
Dupin cyclides and geometric inversions
An advantage for investigations of cyclides is the property:
(I): Any Dupin cyclide is the image either of a right circular cylinder or a right circular double cone or a torus of revolution by an inversion (reflection at a sphere).The inversion at the sphere with equation
The most important properties of an inversion at a sphere are:
- Spheres and circles are mapped on the same objects.
- Planes and lines containing the origin (center of inversion) are mapped on themselves.
- Planes and lines not containing the origin are mapped on spheres or circles passing the origin.
- An inversion is involutory (identical with the inverse mapping).
- An inversion preserves angles.
One can map arbitrary surfaces by an inversion. The formulas above give in any case parametric or implicit representations of the image surface, if the surfaces are given parametrically or implicitly. In case of a parametric surface one gets:
But: Only in case of right circular cylinders and cones and tori of revolution one gets Dupin cyclides and vice versa.
Example cylinder
a) Because lines, which do not contain the origin, are mapped by an inversion at a sphere (in picture: magenta) on circles containing the origin the image of the cylinder is a ring cyclide with mutually touching circles at the origin. As the images of the line segments, shown in the picture, there appear on line circle segments as images. The spheres which touch the cylinder on the inner side are mapped on a first pencil of spheres which generate the cyclide as a canal surface. The images of the tangent planes of the cylinder become the second pencil of spheres touching the cyclide. The latter ones pass through the origin.
b) The second example inverses a cylinder that contains the origin. Lines passing the origin are mapped onto themselves. Hence the surface is unbounded and a parabolic cyclide.
Example cone
The lines generating the cone are mapped on circles, which intersect at the origin and the image of the cone's vertex. The image of the cone is a double horn cyclide. The picture shows the images of the line segments (of the cone), which are circles segments, actually.
Example torus
Both the pencils of circles on the torus (shown in the picture) are mapped on the corresponding pencils of circles on the cyclide. In case of a self-intersecting torus one would get a spindle cyclide.
Separation of variables
Dupin cyclides are a special case of a more general notion of a cyclide, which is a natural extension of the notion of a quadric surface. Whereas a quadric can be described as the zero-set of second order polynomial in Cartesian coordinates (x1,x2,x3), a cyclide is given by the zero-set of a second order polynomial in (x1,x2,x3,r2), where r2=x12+x22+x32. Thus it is a quartic surface in Cartesian coordinates, with an equation of the form:
where Q is a 3x3 matrix, P and R are a 3-dimensional vectors, and A and B are constants.
Families of cyclides give rise to various cyclidic coordinate geometries.
In Maxime Bôcher's 1891 dissertation, Ueber die Reihenentwickelungen der Potentialtheorie, it was shown that the Laplace equation in three variables can be solved using separation of variables in 17 conformally distinct quadric and cyclidic coordinate geometries. Many other cyclidic geometries can be obtained by studying R-separation of variables for the Laplace equation.
