 | ||
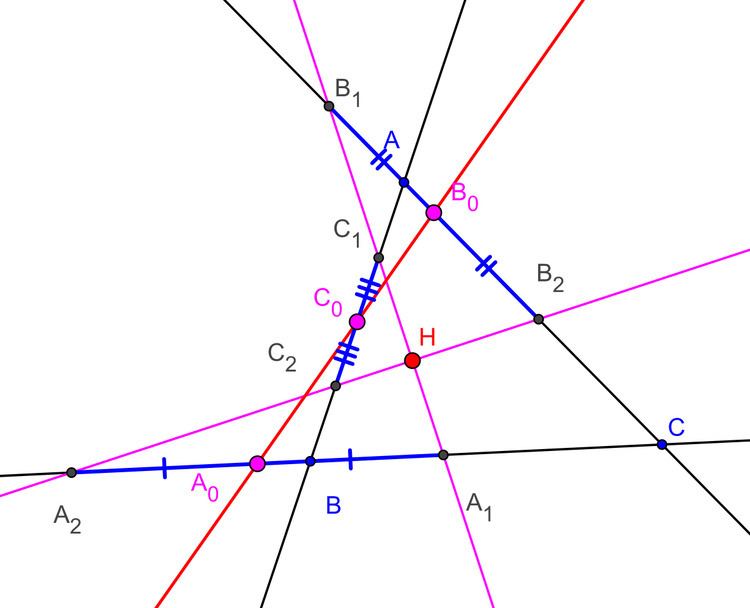
In Euclidean geometry, the Droz-Farny line theorem is a property of two perpendicular lines through the orthocenter of an arbitrary triangle.
Contents
Let
The theorem was stated by Arnold Droz-Farny in 1899, but it is not clear whether he had a proof.
Goormaghtigh's generalization
A generalization of the Droz-Farny line theorem was proved in 1930 by René Goormaghtigh.
As above, let
The Droz-Farny line theorem is a special case of this result, when
Dao's generalization
The theorem was further generalized by Dao Thanh Oai. The generalization as follows:
First generalization: Let P be a point on the plane, let three parallel segments AA', BB', CC' such that its midpoints and P are collinear. Then 'PA', PB', PC' meet BC, CA, AB respectively at three collinear points.
Second generalization: Let a conic S and a point P on the plane. Construct three lines da, db, dc through P such that they meet the conic at A, A'; B, B' ; C, C' respectively. Let D be a point on the polar of point P with respect to (S) or D lies on the conic (S). Let DA' ∩ BC =A0; DB' ∩ AC = B0; DC' ∩ AB= C0. Then A0, B0, C0 are collinear.
