Discrete measure

Definition and properties

A measure μ defined on the Lebesgue measurable sets of the real line with values in [ 0 , ∞ ] is said to be discrete if there exists a (possibly finite) sequence of numbers

such that

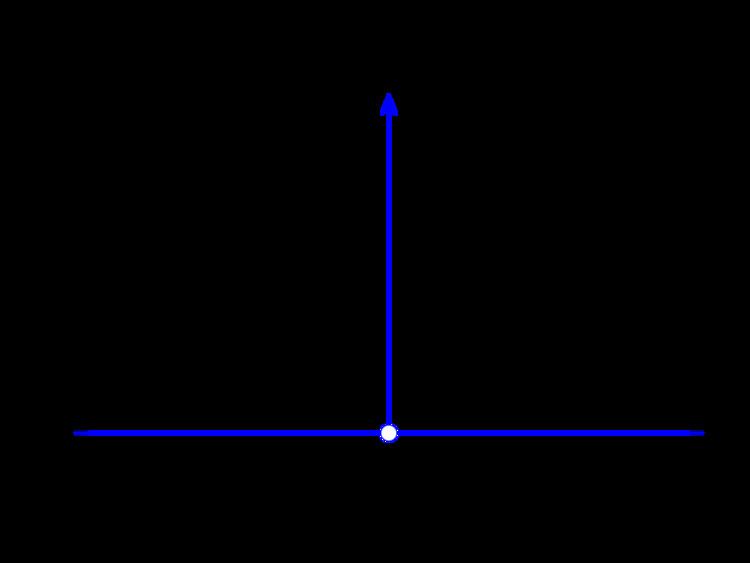
The simplest example of a discrete measure on the real line is the Dirac delta function δ . One has δ ( R ∖ { 0 } ) = 0 and δ ( { 0 } ) = 1.

More generally, if s 1 , s 2 , … is a (possibly finite) sequence of real numbers, a 1 , a 2 , … is a sequence of numbers in [ 0 , ∞ ] of the same length, one can consider the Dirac measures δ s i defined by

for any Lebesgue measurable set X . Then, the measure

is a discrete measure. In fact, one may prove that any discrete measure on the real line has this form for appropriately chosen sequences s 1 , s 2 , … and a 1 , a 2 , …

Extensions

One may extend the notion of discrete measures to more general measure spaces. Given a measure space ( X , Σ ) , and two measures μ and ν on it, μ is said to be discrete in respect to ν if there exists an at most countable subset S of X such that

1. All singletons { s } with s in S are measurable (which implies that any subset of S is measurable)
2. ν ( S ) = 0
3. μ ( X ∖ S ) = 0.

Notice that the first two requirements are always satisfied for an at most countable subset of the real line if ν is the Lebesgue measure, so they were not necessary in the first definition above.

As in the case of measures on the real line, a measure μ on ( X , Σ ) is discrete in respect to another measure ν on the same space if and only if μ has the form

where S = { s 1 , s 2 , … } , the singletons { s i } are in Σ , and their ν measure is 0.

One can also define the concept of discreteness for signed measures. Then, instead of conditions 2 and 3 above one should ask that ν be zero on all measurable subsets of S and μ be zero on measurable subsets of X ∖ S .