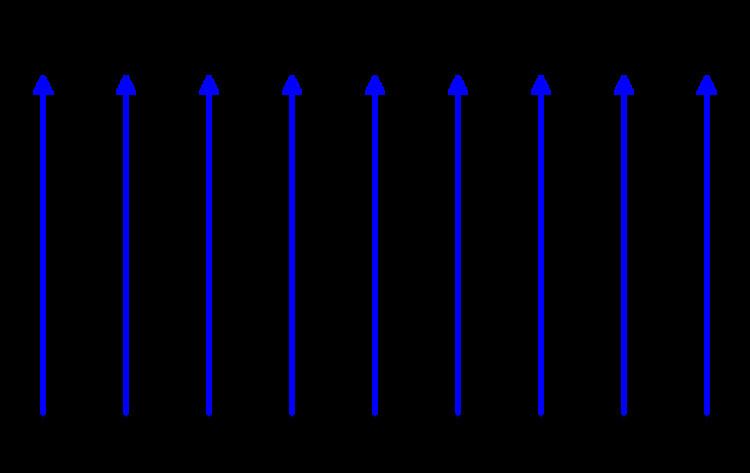
Dirac comb - Alchetron, The Free Social Encyclopedia

In mathematics, a Dirac comb (also known as an impulse train and sampling function in electrical engineering) is a periodic tempered distribution constructed from Dirac delta functions

for some given period T. The symbol III ⁡ ( t ) , where the period is omitted, represents a Dirac comb of unit period. Some authors, notably Bracewell as well as some textbook authors in electrical engineering and circuit theory, refer to it as the Shah function (possibly because its graph resembles the shape of the Cyrillic letter sha Ш). Because the Dirac comb function is periodic, it can be represented as a Fourier series:

III T ⁡ ( t ) = 1 T ∑ n = − ∞ ∞ e 2 π i n t T .

The Dirac comb function allows one to represent both continuous and discrete phenomena, such as sampling and aliasing, in a single framework of continuous Fourier analysis on Schwartz distributions, without any reference to Fourier series. Owing to the Poisson summation formula, in signal processing, the Dirac comb allows modelling sampling via multiplication with it, but it also allows modelling periodization via convolution with it.

Dirac Comb Identity

The Dirac comb can be constructed in two ways, either by using the comb operator (performing sampling) applied to the function that is constantly 1 , or, alternatively, by using the rep operator (performing periodization) applied to the Dirac delta δ . Formally, this yields

comb T ⁡ { 1 } = III T = rep T ⁡ { δ }

where

comb T ⁡ { f ( t ) } = d e f ∑ k = − ∞ ∞ f ( k T ) δ ( t − k T ) and rep T ⁡ { g ( t ) } = d e f ∑ k = − ∞ ∞ g ( t − k T ) (Woodward 1953), (Brandwood 2003).

In signal processing, this property on one hand allows sampling a function f ( t ) via multiplication with III T , and on the other hand it also allows the periodization of f ( t ) via convolution with III T (Bracewell 1986).

Scaling

The scaling property of the Dirac comb follows from the properties of the Dirac delta function. Since δ ( t ) = 1 a δ ( t a ) for positive real numbers a , it follows that:

III T ⁡ ( t ) = 1 T III ⁡ ( t T ) III a T ⁡ ( t ) = 1 a III T ⁡ ( t a )

Note that requiring positive scaling numbers a instead of negative ones is no restriction because the negative sign would only reverse the summation within III T but not the result of the summation.

Fourier series

It is clear that III T ⁡ ( t ) is periodic with period T . That is

III T ⁡ ( t + T ) = III T ⁡ ( t )

for all t. The complex Fourier series for such a periodic function is

III T ⁡ ( t ) = ∑ n = − ∞ + ∞ c n e 2 π i n t T

where the Fourier coefficients, c_n are

c n = 1 T ∫ t 0 t 0 + T III T ⁡ ( t ) e − 2 π i n t T d t ( − ∞ < t 0 < + ∞ ) = 1 T ∫ − T 2 T 2 III T ⁡ ( t ) e − 2 π i n t T d t = 1 T ∫ − T 2 T 2 δ ( t ) e − 2 π i n t T d t = 1 T e − 2 π i n 0 T = 1 T .

All Fourier coefficients are 1/T resulting in

III T ⁡ ( t ) = 1 T ∑ n = − ∞ ∞ e 2 π i n t T .

Fourier transform

The Fourier transform of a Dirac comb is also a Dirac comb. This is evident when one considers that all the Fourier components add constructively whenever f is an integer multiple of 1 T .

Unitary transform to ordinary frequency domain (Hz):

III T ⁡ ( t ) ⟷ F T III 1 T ⁡ ( f ) = ∑ n = − ∞ ∞ e − i 2 π f n T .

Notably, the unit period Dirac comb transforms to itself:

III ⁡ ( t ) ⟷ F III ⁡ ( f )

Unitary transform to angular frequency domain (radian/s):

III T ⁡ ( t ) ⟷ F 2 π T III 2 π T ⁡ ( ω ) = 1 2 π ∑ n = − ∞ ∞ e − i ω n T .

Sampling and aliasing

Multiplying any function by a Dirac comb transforms it into a train of impulses with integrals equal to the value of the function at the nodes of the comb. This operation is frequently used to represent sampling.

( III T ⁡ x ) ( t ) = ∑ k = − ∞ ∞ x ( t ) δ ( t − k T ) = ∑ k = − ∞ ∞ x ( k T ) δ ( t − k T ) .

Due to the self-transforming property of the Dirac comb and the convolution theorem, this corresponds to convolution with the Dirac comb in the frequency domain.

III T ⁡ x ⟷ F 1 T III 1 T ∗ X

Since convolution with a delta function δ ( t − k T ) is equivalent to shifting the function by k T , convolution with the Dirac comb corresponds to replication or periodic summation:

( III 1 T ∗ X ) ( f ) = ∑ k = − ∞ ∞ X ( f − k T )

This leads to a natural formulation of the Nyquist-Shannon sampling theorem. If the spectrum of the function x contains no frequencies higher than B (i.e., its spectrum is nonzero only in the interval ( − B , B ) ) then samples of the original function at intervals 1 / 2 B are sufficient to reconstruct the original signal. It suffices to multiply the spectrum of the sampled function by a suitable rectangle function, which is equivalent to applying a brick-wall lowpass filter.

III 1 2 B ⁡ x ⟷ F 2 B III 2 B ∗ X 1 2 B Π ( t 2 B ) ( 2 B III 2 B ∗ X ) = X

In the time domain, this multiplication is equivalent to convolving a sinc function with the samples of the signal, leading to the Whittaker–Shannon interpolation formula.

Use in directional statistics

In directional statistics, the Dirac comb of period 2π is equivalent to a wrapped Dirac delta function, and is the analog of the Dirac delta function in linear statistics.

In linear statistics, the random variable (x) is usually distributed over the real number line, or some subset thereof, and the probability density of x is a function whose domain is the set real numbers, and whose integral from − ∞ to + ∞ is unity. In directional statistics, the random variable (θ) is distributed over the unit circle and the probability density of θ is a function whose domain is some interval of the real numbers of length 2π and whose integral over that interval is unity. Just as the integral of the product of a Dirac delta function with an arbitrary function over the real number line yields the value of that function at zero, so the integral of the product of a Dirac comb of period 2π with an arbitrary function of period 2π over the unit circle yields the value of that function at zero.

References

Dirac comb Wikipedia

(Text) CC BY-SA

Contents