Density of air

Density of air calculations

Depending on the measuring instruments, use, area of expertise and necessary rigor of the result different calculation criteria and sets of equations for the calculation of the density of air are used. This topic are some examples of calculations with the main variables involved, the amounts presented throughout these examples are properly referenced usual values, different values can be found in other references depending on the criteria used for the calculation . Furthermore we must pay attention to the fact that air is a mixture of gases and the calculation always simplify, to a greater or lesser extent, the properties of the mixture and the values for the composition according to the criteria of calculation.

Temperature and pressure

The density of dry air can be calculated using the ideal gas law, expressed as a function of temperature and pressure:

ρ = p R s p e c i f i c T

where:

ρ = air density (kg/m³) p = absolute pressure (Pa) T = absolute temperature (K) R s p e c i f i c = specific gas constant for dry air (J/(kg·K))

The specific gas constant for dry air is 287.058 J/(kg·K) in SI units, and 53.35 (ft·lbf)/(lb·°R) in United States customary and Imperial units. This quantity may vary slightly depending on the molecular composition of air at a particular location.

Therefore:

At IUPAC standard temperature and pressure (0 °C and 100 kPa), dry air has a density of 1.2754 kg/m³.

At 20 °C and 101.325 kPa, dry air has a density of 1.2041 kg/m³.

At 70 °F and 14.696 psi, dry air has a density of 0.074887 lb/ft³.

The following table illustrates the air density–temperature relationship at 1 atm or 101.325 kPa:

Humidity (water vapor)

The addition of water vapor to air (making the air humid) reduces the density of the air, which may at first appear counter-intuitive. This occurs because the molar mass of water (18 g/mol) is less than the molar mass of dry air (around 29 g/mol). For any gas, at a given temperature and pressure, the number of molecules present is constant for a particular volume (see Avogadro's Law). So when water molecules (water vapor) are added to a given volume of air, the dry air molecules must decrease by the same number, to keep the pressure or temperature from increasing. Hence the mass per unit volume of the gas (its density) decreases.

The density of humid air may be calculated as a mixture of ideal gases. In this case, the partial pressure of water vapor is known as the vapor pressure. Using this method, error in the density calculation is less than 0.2% in the range of −10 °C to 50 °C. The density of humid air is found by:

ρ h u m i d   a i r = p d R d T + p v R v T = p d M d + p v M v R T   

where:

ρ h u m i d   a i r = Density of the humid air (kg/m³) p d = Partial pressure of dry air (Pa) R d = Specific gas constant for dry air, 287.058 J/(kg·K) T = Temperature (K) p v = Pressure of water vapor (Pa) R v = Specific gas constant for water vapor, 461.495 J/(kg·K) M d = Molar mass of dry air, 0.028964 kg/mol M v = Molar mass of water vapor, 0.018016 kg/mol R = Universal gas constant, 8.314 J/(K·mol)

The vapor pressure of water may be calculated from the saturation vapor pressure and relative humidity. It is found by:

p v = ϕ p s a t

where:

p v = Vapor pressure of water ϕ = Relative humidity p s a t = Saturation vapor pressure

The saturation vapor pressure of water at any given temperature is the vapor pressure when relative humidity is 100%. One formula used to find the saturation vapor pressure is:

p s a t = 6.1078 × 10 7.5 T T + 237.3

where T = is in degrees C.

note:

This equation will give the result of pressure in hPa (100 Pa, equivalent to the older unit millibar, 1 mbar = 0.001 bar = 0.1 kPa)

The partial pressure of dry air p d is found considering partial pressure, resulting in:

p d = p − p v

Where p simply denotes the observed absolute pressure.

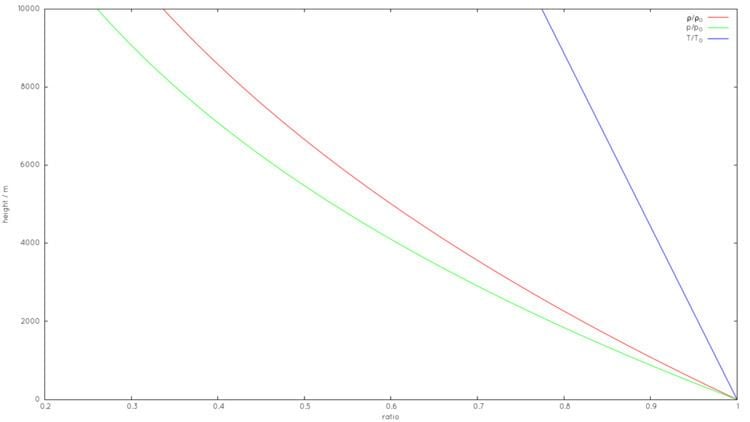
Altitude

To calculate the density of air as a function of altitude, one requires additional parameters. They are listed below, along with their values according to the International Standard Atmosphere, using for calculation the universal gas constant instead of the air specific constant:

p 0 = sea level standard atmospheric pressure, 101.325 kPa T 0 = sea level standard temperature, 288.15 K g = earth-surface gravitational acceleration, 9.80665 m/s² L = temperature lapse rate, 0.0065 K/m R = ideal (universal) gas constant, 8.31447 J/(mol·K) M = molar mass of dry air, 0.0289644 kg/mol

Temperature at altitude h meters above sea level is approximated by the following formula (only valid inside the troposphere):

T = T 0 − L h

The pressure at altitude h is given by:

p = p 0 ( 1 − L h T 0 ) g M R L

Density can then be calculated according to a molar form of the ideal gas law:

ρ = p M R T

where:

M = molar mass R = ideal gas constant T = absolute temperature p = absolute pressure

Composition

The air composition adopted for each set of equations varies with the references used in the table below are listed some examples of air composition according to the references. Despite minor differences to define all formulations the predicted molar mass of dry air and below table shows these differences. Importantly, some of the examples are not normalized so that the composition is equal to unity (100%), before they used should be normalized.