This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.
^α The source that is used for these formulae uses
θ for the azimuthal angle and
φ for the polar angle, which is common mathematical notation. This page uses
θ for the polar angle and
φ for the azimuthal angle, which is common notation in physics. In order to get the mathematics formulae, switch
θ and
φ in the formulae shown in the table above.
- div grad f ≡ ∇ ⋅ ∇ f ≡ ∇ 2 f
- curl grad f ≡ ∇ × ∇ f = 0
- div curl A ≡ ∇ ⋅ ( ∇ × A ) = 0
- curl curl A ≡ ∇ × ( ∇ × A ) = ∇ ( ∇ ⋅ A ) − ∇ 2 A (Lagrange's formula for del)
- ∇ 2 ( f g ) = f ∇ 2 g + 2 ∇ f ⋅ ∇ g + g ∇ 2 f
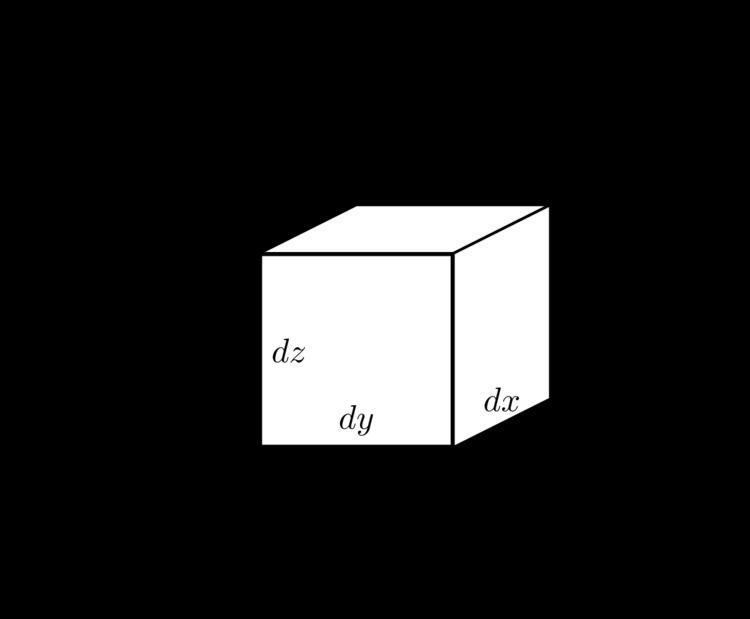
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A x ( x + d x ) d y d z − A x ( x ) d y d z + A y ( y + d y ) d x d z − A y ( y ) d x d z + A z ( z + d z ) d x d y − A z ( z ) d x d y d x d y d z = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z
( curl A ) x = lim S ⊥ x ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( y + d y ) d z − A z ( y ) d z + A y ( z ) d y − A y ( z + d z ) d y d y d z = ∂ A y ∂ z − ∂ A z ∂ y
The expressions for ( curl A ) y and ( curl A ) z are found in the same way.
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A ρ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ d z − A ρ ( ρ ) ρ d ϕ d z + A ϕ ( ϕ + d ϕ ) d ρ d z − A ϕ ( ϕ ) d ρ d z + A z ( z + d z ) d ρ ρ d ϕ − A z ( z ) d ρ ρ d ϕ d ρ ρ d ϕ d z = 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A ϕ ∂ ϕ + ∂ A z ∂ z
( curl A ) ρ = lim S ⊥ ρ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A r ( r + d r ) ( r + d r ) d θ ( r + d r ) sin θ d ϕ − A r ( r ) r d θ r sin θ d ϕ + . . . d r r d θ r sin θ d ϕ = 1 r 2 ∂ ( r 2 A r ) ∂ r + . . .
( curl A ) r = lim S ⊥ r ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A θ ( ϕ ) r d θ + A ϕ ( θ + d θ ) r sin ( θ + d θ ) d ϕ − A θ ( ϕ + d ϕ ) r d θ − A ϕ ( θ ) r sin θ d ϕ r d θ r sin θ d ϕ = 1 r sin θ ∂ ( sin ( θ ) A ϕ ) ∂ θ − 1 r sin θ ∂ A θ ∂ ϕ