Neha Patil (Editor)

Degree (graph theory)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Degree (graph theory)

In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted deg ⁡ ( v ) or deg ⁡ v . The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.

Contents

Handshaking lemma

The degree sum formula states that, given a graph G = ( V , E ) ,

∑ v ∈ V deg ⁡ ( v ) = 2 | E | .

The formula implies that in any graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.

Degree sequence

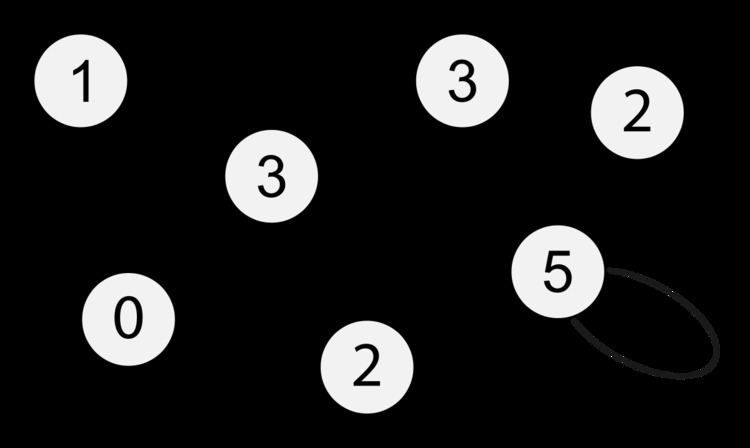
The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.

The degree sequence problem is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence. As a consequence of the degree sum formula, any sequence with an odd sum, such as (3, 3, 1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a multigraph. The construction of such a graph is straightforward: connect vertices with odd degrees in pairs by a matching, and fill out the remaining even degree counts by self-loops. The question of whether a given degree sequence can be realized by a simple graph is more challenging. This problem is also called graph realization problem and can either be solved by the Erdős–Gallai theorem or the Havel–Hakimi algorithm. The problem of finding or estimating the number of graphs with a given degree sequence is a problem from the field of graph enumeration.

Special values

  • A vertex with degree 0 is called an isolated vertex.
  • A vertex with degree 1 is called a leaf vertex or end vertex, and the edge incident with that vertex is called a pendant edge. In the graph on the right, {3,5} is a pendant edge. This terminology is common in the study of trees in graph theory and especially trees as data structures.
  • A vertex with degree n − 1 in a graph on n vertices is called a dominating vertex.

    • Global properties

  • If each vertex of the graph has the same degree k the graph is called a k-regular graph and the graph itself is said to have degree k. Similarly, a bipartite graph in which every two vertices on the same side of the bipartition as each other have the same degree is called a biregular graph.
  • An undirected, connected graph has an Eulerian path if and only if it has either 0 or 2 vertices of odd degree. If it has 0 vertices of odd degree, the Eulerian path is an Eulerian circuit.
  • A directed graph is a pseudoforest if and only if every vertex has outdegree at most 1. A functional graph is a special case of a pseudoforest in which every vertex has outdegree exactly 1.
  • By Brooks' theorem, any graph other than a clique or an odd cycle has chromatic number at most Δ, and by Vizing's theorem any graph has chromatic index at most Δ + 1.
  • A k-degenerate graph is a graph in which each subgraph has a vertex of degree at most k.

    • References

    Degree (graph theory) Wikipedia
    (Text) CC BY-SA


    Similar Topics