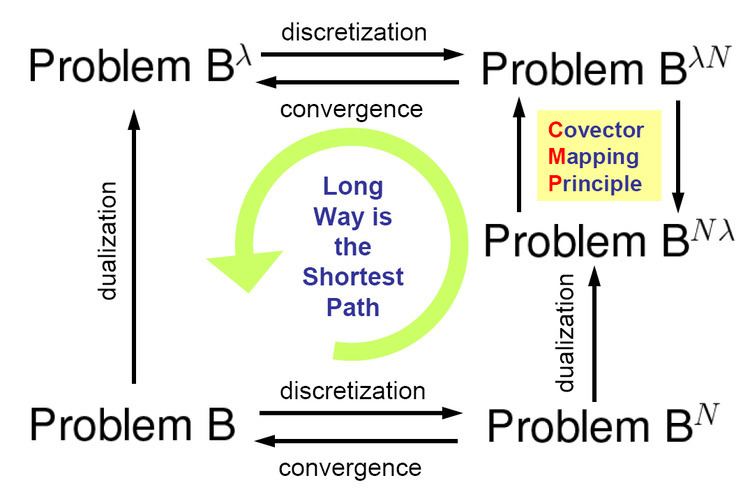
The covector mapping principle is a special case of Riesz' representation theorem, which is a fundamental theorem in functional analysis. The name was coined by Ross and co-workers, It provides conditions under which dualization can be commuted with discretization in the case of computational optimal control.
An application of Pontryagin's minimum principle to Problem B , a given optimal control problem generates a boundary value problem. According to Ross, this boundary value problem is a Pontryagin lift and is represented as Problem B λ .
Now suppose one discretizes Problem B λ . This generates Problem B λ N where N represents the number of discrete pooints. For convergence, it is necessary to prove that as
N → ∞ , Problem B λ N → Problem B λ In the 1960s Kalman and others showed that solving Problem B λ N is extremely difficult. This difficulty, known as the curse of complexity, is complementary to the curse of dimensionality.
In a series of papers starting in the late 1990s, Ross and Fahroo showed that one could arrive at a solution to Problem B λ (and hence Problem B ) more easily by discretizing first (Problem B N ) and dualizing afterwards (Problem B N λ ). The sequence of operations must be done carefully to ensure consistency and convergence. The covector mapping principle asserts that a covector mapping theorem can be discovered to map the solutions of Problem B N λ to Problem B λ N thus completing the circuit.