 | ||
In probability theory and statistics, a copula is a multivariate probability distribution for which the marginal probability distribution of each variable is uniform. Copulas are used to describe the dependence between random variables. Their name comes from the Latin for "link" or "tie", similar but unrelated to grammatical copulas in linguistics. Copulas have been used widely in quantitative finance to model and minimize tail risk and portfolio optimization applications.
Contents
- Mathematical definition
- Definition
- Sklars theorem
- FrchetHoeffding copula bounds
- Families of copulas
- Gaussian copula
- Archimedean copulas
- Most important Archimedean copulas
- Expectation for copula models and Monte Carlo integration
- Empirical copulas
- Quantitative finance
- Civil engineering
- Reliability engineering
- Warranty data analysis
- Turbulent combustion
- Medicine
- Climate and weather research
- Random vector generation
- References
Sklar's Theorem states that any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the variables.
Copulas are popular in high-dimensional statistical applications as they allow one to easily model and estimate the distribution of random vectors by estimating marginals and copulae separately. There are many parametric copula families available, which usually have parameters that control the strength of dependence. Some popular parametric copula models are outlined below.
Mathematical definition
Consider a random vector
has uniformly distributed marginals.
The copula of
The copula C contains all information on the dependence structure between the components of
The importance of the above is that the reverse of these steps can be used to generate pseudo-random samples from general classes of multivariate probability distributions. That is, given a procedure to generate a sample
The inverses
Definition
In probabilistic terms,
In analytic terms,
For instance, in the bivariate case,
Sklar's theorem
Sklar's theorem, named after Abe Sklar, provides the theoretical foundation for the application of copulas. Sklar's theorem states that every multivariate cumulative distribution function
of a random vector
In case that the multivariate distribution has a density
where
The theorem also states that, given
The converse is also true: given a copula
Fréchet–Hoeffding copula bounds
The Fréchet–Hoeffding Theorem (after Maurice René Fréchet and Wassily Hoeffding ) states that for any Copula
The function W is called lower Fréchet–Hoeffding bound and is defined as
The function M is called upper Fréchet–Hoeffding bound and is defined as
The upper bound is sharp: M is always a copula, it corresponds to comonotone random variables.
The lower bound is point-wise sharp, in the sense that for fixed u, there is a copula
In two dimensions, i.e. the bivariate case, the Fréchet–Hoeffding Theorem states
Families of copulas
Several families of copulae have been described.
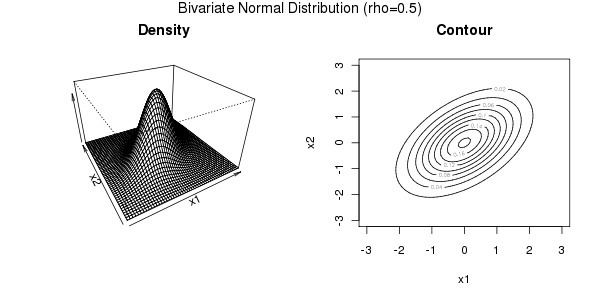
Gaussian copula
The Gaussian copula is a distribution over the unit cube
For a given correlation matrix
where
where
Archimedean copulas
Archimedean copulas are an associative class of copulas. Most common Archimedean copulas admit an explicit formula, something not possible for instance for the Gaussian copula. In practice, Archimedean copulas are popular because they allow modeling dependence in arbitrarily high dimensions with only one parameter, governing the strength of dependence.
A copula C is called Archimedean if it admits the representation
where
Moreover, the above formula for C yields a copula for
for all
Most important Archimedean copulas
The following tables highlight the most prominent bivariate Archimedean copulas, with their corresponding generator. Note that not all of them are completely monotone, i.e. d-monotone for all
Expectation for copula models and Monte Carlo integration
In statistical applications, many problems can be formulated in the following way. One is interested in the expectation of a response function
If
this expectation can be rewritten as
In case the copula C is absolutely continuous, i.e. C has a density c, this equation can be written as
and if each marginal distribution has the density
If copula and margins are known (or if they have been estimated), this expectation can be approximated through the following Monte Carlo algorithm:
- Draw a sample
( U 1 k , … , U d k ) ∼ C ( k = 1 , … , n ) of size n from the copula C - By applying the inverse marginal cdf's, produce a sample of
( X 1 , … , X d ) by setting( X 1 k , … , X d k ) = ( F 1 − 1 ( U 1 k ) , … , F d − 1 ( U d k ) ) ∼ H ( k = 1 , … , n ) - Approximate
E [ g ( X 1 , … , X d ) ] by its empirical value:
Empirical copulas
When studying multivariate data, one might want to investigate the underlying copula. Suppose we have observations
from a random vector
However, the marginal distribution functions
instead. Then, the pseudo copula observations are defined as
The corresponding empirical copula is then defined as
The components of the pseudo copula samples can also be written as
Therefore, the empirical copula can be seen as the empirical distribution of the rank transformed data.
Quantitative finance
In risk/portfolio management, copulas are used to perform stress-tests and robustness checks that are especially important during “downside/crisis/panic regimes” where extreme downside events may occur (e.g., the global financial crisis of 2007–2008).
The formula was also adapted for financial markets and was used to estimate the probability distribution of losses on pools of loans or bonds. The users of the formula have been criticized for creating "evaluation cultures" that continued to use simple copulæ despite the simple versions being acknowledged as inadequate for that purpose. During a downside regime, a large number of investors who have held positions in riskier assets such as equities or real estate may seek refuge in ‘safer’ investments such as cash or bonds. This is also known as a flight-to-quality effect and investors tend to exit their positions in riskier assets in large numbers in a short period of time. As a result, during downside regimes, correlations across equities are greater on the downside as opposed to the upside and this may have disastrous effects on the economy. For example, anecdotally, we often read financial news headlines reporting the loss of hundreds of millions of dollars on the stock exchange in a single day; however, we rarely read reports of positive stock market gains of the same magnitude and in the same short time frame.
Copulas are useful in portfolio/risk management and help us analyse the effects of downside regimes by allowing the modelling of the marginals and dependence structure of a multivariate probability model separately. For example, consider the stock exchange as a market consisting of a large number of traders each operating with his/her own strategies to maximize profits. The individualistic behaviour of each trader can be described by modelling the marginals. However, as all traders operate on the same exchange, each trader's actions have an interaction effect with other traders'. This interaction effect can be described by modelling the dependence structure. Therefore, copulas allow us to analyse the interaction effects which are of particular interest during downside regimes as investors tend to herd their trading behaviour and decisions.
Previously, scalable copula models for large dimensions only allowed the modelling of elliptical dependence structures (i.e., Gaussian and Student-t copulas) that do not allow for correlation asymmetries where correlations differ on the upside or downside regimes. However, the recent development of vine copulas (also known as pair copulas) enables the flexible modelling of the dependence structure for portfolios of large dimensions. The Clayton canonical vine copula allows for the occurrence of extreme downside events and has been successfully applied in portfolio choice and risk management applications. The model is able to reduce the effects of extreme downside correlations and produces improved statistical and economic performance compared to scalable elliptical dependence copulas such as the Gaussian and Student-t copula. Other models developed for risk management applications are panic copulas that are glued with market estimates of the marginal distributions to analyze the effects of panic regimes on the portfolio profit and loss distribution. Panic copulas are created by Monte Carlo simulation, mixed with a re-weighting of the probability of each scenario.
As far as derivatives pricing is concerned, dependence modelling with copula functions is widely used in applications of financial risk assessment and actuarial analysis – for example in the pricing of collateralized debt obligations (CDOs). Some believe the methodology of applying the Gaussian copula to credit derivatives to be one of the reasons behind the global financial crisis of 2008–2009. Despite this perception, there are documented attempts of the financial industry, occurring before the crisis, to address the limitations of the Gaussian copula and of copula functions more generally, specifically the lack of dependence dynamics. The Gaussian copula is lacking as it only allows for an elliptical dependence structure, as dependence is only modeled using the variance-covariance matrix. This methodology is limited such that it does not allow for dependence to evolve as the financial markets exhibit asymmetric dependence, whereby correlations across assets significantly increase during downturns compared to upturns. Therefore, modeling approaches using the Gaussian copula exhibit a poor representation of extreme events. There have been attempts to propose models rectifying some of the copula limitations.
While the application of copulas in credit has gone through popularity as well as misfortune during the global financial crisis of 2008–2009, it is arguably an industry standard model for pricing CDOs. Copulas have also been applied to other asset classes as a flexible tool in analyzing multi-asset derivative products. The first such application outside credit was to use a copula to construct an implied basket volatility surface, taking into account the volatility smile of basket components. Copulas have since gained popularity in pricing and risk management of options on multi-assets in the presence of volatility smile/skew, in equity, foreign exchange and fixed income derivative business. Some typical example applications of copulas are listed below:
Civil engineering
Recently, copula functions have been successfully applied to the database formulation for the reliability analysis of highway bridges, and to various multivariate simulation studies in civil, mechanical and offshore engineering. Researchers are also trying these functions in field of transportation to understand interaction of individual driver behavior components which in totality shapes up the nature of an entire traffic flow.
Reliability engineering
Copulas are being used for reliability analysis of complex systems of machine components with competing failure modes.
Warranty data analysis
Copulas are being used for warranty data analysis in which the tail dependence is analysed
Turbulent combustion
Copulas are used in modelling turbulent partially premixed combustion, which is common in practical combustors.
Medicine
Copula functions have been successfully applied to the analysis of neuronal dependencies and spike counts in neuroscience
Climate and weather research
Copulas have been extensively used in climate- and weather-related research.
Random vector generation
Large synthetic traces of vectors and stationary time series can be generated using empirical copula while preserving the entire dependence structure of small datasets. Such empirical traces are useful in various simulation-based performance studies.
