Grammars with prescribed sequences are grammars in which the sequence of rule application is constrained in some way. There are four different versions of prescribed sequence grammars: language controlled grammars (often called just controlled grammars), matrix grammars, vector grammars, and programmed grammars.
In the standard context-free grammar formalism, a grammar itself is viewed as a 4-tuple, G = ( N , T , S , P ) , where N is a set of non-terminal/phrasal symbols, T is a disjoint set of terminal/word symbols, S is a specially designated start symbol chosen from N, and P is a set of production rules like X → α , where X is some member of N, and α is some member of ( N ∪ T ) ∗ .
Productions over such a grammar are sequences of rules in P that, when applied in order of the sequence, lead to a terminal string. That is, one can view the set of imaginable derivations in G as the set { p 1 p 2 . . . p n : n ≥ 0 } , and the language of G as being the set of terminal strings L ( G ) = { w ∈ T ∗ : S ⇒ p 1 . . . ⇒ p n w } . Control grammars take seriously this definition of the language generated by a grammar, concretizing the set-of-derivations as an aspect of the grammar. Thus, a prescribed sequence controlled grammar is at least approximately a 5-tuple G = ( N , T , S , P , R ) where everything except R is the same as in a CFG, and R is an infinite set of valid derivation sequences p 1 p 2 . . . p n .
The set R, due to its infinitude, is almost always (though not necessarily) described via some more convenient mechanism, such as a grammar (as in language controlled grammars), or a set of matrices or vectors (as in matrix and vector grammars). The different variations of prescribed sequence grammars thus differ by how the sequence of derivations is defined on top of the context-free base. Because matrix grammars and vector grammars are essentially special cases of language controlled grammars, examples of the former two will not be provided below.
Language controlled grammars are grammars in which the production sequences constitute a well-defined language of arbitrary nature, usually though not necessarily regular, over a set of (again usually though not necessarily) context-free production rules. They also often have a sixth set in the grammar tuple, making it G = ( N , T , S , P , R , F ) , where F is a set of productions that are allowed to apply vacuously. This version of language controlled grammars, ones with what is called "appearance checking", is the one henceforth.
We let a regularly controlled context-free grammar with appearance checking be a 6-tuple G = ( N , T , S , P , R , F ) where N, T, S, and P are defined as in CFGs, R is a subset of P* constituting a regular language over P, and F is some subset of P. We then define the immediately derives relation ⇒ p i as follows:
Given some strings x and y, both in ( N ∪ T ) ∗ , and some rule p = A → w ∈ P ,
x ⇒ p a c y holds if either
x = x 1 A x 2 and
y = y 1 w y 2 , or
x = y and
p ∈ F Intuitively, this simply spells out that a rule can apply to a string if the rule's left-hand-side appears in that string, or if the rule is in the set of "vacuously applicable" rules which can "apply" to a string without changing anything. This requirement that the non-vacuously applicable rules must apply is the appearance checking aspect of such a grammar. The language for this kind of grammar is then simply set of terminal strings L ( G ) = { w ∈ T ∗ : S ⇒ p 1 a c w 1 ⇒ p 2 a c w 2 ⇒ p 3 a c . . . ⇒ p n a c w , f o r s o m e p 1 p 2 . . . p n ∈ R } .
Let's consider a simple (though not the simplest) context-free grammar that generates the language { a n : n ≥ 1 } :
Let G = ( { S , A , X } , { a } , S , { f , g , h , k , l } ) , where
f : S → A A g : S → X h : A → S k : A → X l : S → a In language controlled form, this grammar is simply G ′ = ( { S , A , X } , { a } , S , { f , g , h , k , l } , ( f | g | h | k | l ) ∗ , { f , g , h , k , l } ) (where ( f | g | h | k | l ) ∗ is a regular expression denoting the set of all sequences of production rules). A simple modification to this grammar, changing is control sequence set R into the set ( f ∗ g h ∗ k ) ∗ l ∗ , and changing its vacuous rule set F to { g , k } , yields a grammar which generates the non-CF language { a 2 n : n ≥ 0 } . To see how, let's consider the general case of some string with n instances of S in it, i.e. S n (the special case S 1 trivially derives the string a which is a 2 0 , an uninteresting fact).
If we chose some arbitrary production sequence f u g h v k . . . , we can consider three possibilities: n = u , n < u , and n > u When n = u we rewrite all n instances of S as AA, by applying rule f to the string u times, and proceed to apply g, which applies vacuously (by virtue of being in F) . When n < u , we rewrite all n instances of S as AA, and then try to perform the n+1 rewrite using rule f, but this fails because there are no more Ss to rewrite, and f is not in F and so cannot apply vacuously, thus when n < u , the derivation fails. Lastly, then n > u , we rewrite u instances of S, leaving at least one instance of S to be rewritten by the subsequent application of g, rewriting S as X. Given that no rule of this grammar ever rewrites X, such a derivation is destined to never produce a terminal string. Thus only derivations with n = u will ever successfully rewrite the string S n . Similar reasoning holds of the number of As and v. In general, then, we can say that the only valid derivations have the structure S n ⇒ f . . . ⇒ f A 2 n ⇒ g A 2 n ⇒ h . . . ⇒ h S 2 n ⇒ k S 2 n will produce terminal strings of the grammar. The X rules, combined with the structure of the control, essentially force all Ss to be rewritten as AAs prior to any As being rewritten as Ss, which again is forced to happen prior to all still later iterations over the S-to-AA cycle. Finally, the Ss are rewritten as as. In this way, the number of Ss doubles each for each instantiation of f 8 g h ∗ k that appears in a terminal-deriving sequence.
Choosing two random non-terminal deriving sequences, and one terminal-deriving one, we can see this in work:
Let s 1 = f f g h k l l , then we get the failed derivation:
S ⇒ f a c A A ⇒ f a c failure: f cannot apply, no S to rewrite Let s 2 = f g h h h k l l , then we get the failed derivation:
S ⇒ f a c A A ⇒ g a c A A ⇒ h a c S A ⇒ h a c S S ⇒ h a c failure: h cannot apply, no A to rewrite Let s 3 = f g h h k l l , then we get the successful derivation:
S ⇒ f a c A A ⇒ g a c A A ⇒ h a c S A ⇒ h a c S S ⇒ k a c S S ⇒ l a c a S ⇒ l a c a a Similar derivations with a second cycle of f ∗ g h ∗ k produce only SSSS. Showing only the (continued) successful derivation:
. . . ⇒ S S ⇒ f a c A A S ⇒ f a c A A A A ⇒ g a c A A A A Matrix grammars (expanded on in their own article) are a special case of regular controlled context-free grammars, in which the production sequence language is of the form ( m 1 | m 2 | . . . | m n ) ∗ , where each "matrix" m i is a single sequence. For convenience, such a grammar is not represented with a grammar over P, but rather with just a set of the matrices in place of both the language and the production rules. Thus, a matrix grammar is the 5-tuple G = ( N , T , M , S , F ) , where N, T, S, and F are defined essentially as previously done (with F a subset of M this time), and M is a set of matrices m i = p i , 1 p i , 2 . . . p i , n i where each p i , j is a context-free production rule.
The derives relation in a matrix grammar is thus defined simply as:
Given some strings x and y, both in ( N ∪ T ) ∗ , and some matrix m = p 1 p 2 . . . p n ∈ M ,
x ⇒ m a c y holds if either
x = x 1 A x 2 ,
y = y 1 w y 2 , and
A ⇒ p 1 a c w 1 ⇒ p 2 a c w 2 ⇒ p 3 a c . . . ⇒ p n a c w , or
x = y and
m ∈ F Informally, a matrix grammar is simply a grammar in which during each rewriting cycle, a particular sequence of rewrite operations must be performed, rather than just a single rewrite operation, i.e. one rule "triggers" a cascade of other rules. Similar phenomena can be performed in the standard context-sensitive idiom, as done in rule-based phonology and earlier Transformational grammar, by what are known as "feeding" rules, which alter a derivation in such a way as to provide the environment for a non-optional rule that immediately follows it.
Vector grammars are closely related to matrix grammars, and in fact can be seen as a special class of matrix grammars, in which if m ∈ M , then so are all of its permutations p ( m ) . For convenience, however, we will define vector grammars as follows: a vector grammar is a 5-tuple G = ( N , T , M , S , F ) , where N, T, and F are defined previously (F being a subset of M again), and where M is a set of vectors m i = { p 1 , p 2 , . . . , p n } , each vector being a set of context free rules.
The derives relation in a vector grammar is then:
Given some strings x and y, both in ( N ∪ T ) ∗ , and some matrix m = { p 1 , p 2 , . . . , p n } ∈ M ,
x ⇒ m a c y holds if either
x = x 1 A x 2 ,
y = y 1 w y 2 , and
A ⇒ p i 1 a c w 1 ⇒ p i 2 a c w 2 ⇒ p i 3 a c . . . ⇒ p i n a c w , where
m = { p i 1 , p i 2 , . . . , p i n } , or
x = y and
m ∈ F Notice that the number of production rules used in the derivation sequence, n, is the same as the number of production rules in the vector. Informally, then, a vector grammar is one in which a set of productions is applied, each production applied exactly once, in arbitrary order, to derive one string from another. Thus vector grammars are almost identical to matrix grammars, minus the restriction on the order in which the productions must occur during each cycle of rule application.
Programmed grammars are relatively simple extensions to context-free grammars with rule-by-rule control of the derivation. A programmed grammar is a 4-tuple G = ( N , T , S , P ) , where N, T, and S are as in a context-free grammar, and P is a set of tuples ( p , σ , ϕ ) , where p is a context-free production rule, σ is a subset of N (called the success field), and ϕ is a subset of N (called the failure field). If the failure field of every rule in P is empty, the grammar lacks appearance checking, and if at least one failure field is not empty, the grammar has appearance checking. The derivation relation on a programmed grammar is defined as follows:
Given two strings x , y ∈ ( N ∪ T ) ∗ , and some rule p = ( A → w , σ , ϕ ) ∈ P ,
x ⇒ p y and
x = x ′ A x ″ , y = x ′ w x ″ , or
x = y and A does not appear in x.
The language of a programmed grammar G is defined by constraining the derivation rule-wise, as L ( G ) = { w ∈ ( N ∪ T ) ∗ : S ⇒ p 1 w 1 ⇒ p 2 . . . ⇒ p n w } , where for each p i = ( A i → v i , σ i , ϕ i ) , either w i − 1 = x i − 1 A x i − 1 ′ , w i = x i − 1 v i x i − 1 ′ , a n d p i + 1 ∈ σ i or w i − 1 = w i , p i + 1 ∈ ϕ i .
Intuitively, when applying a rule p in a programmed grammar, the rule can either succeed at rewriting a symbol in the string, in which case the subsequent rule must be in ps success field, or the rule can fail to rewrite a symbol (thus applying vacuously), in which case the subsequent rule must be in ps failure field. The choice of which rule to apply to the start string is arbitrary, unlike in a language controlled grammar, but once a choice is made the rules that can be applied after it constrain the sequence of rules from that point on.
As with so many controlled grammars, programmed grammars can generate the language { a 2 n : n ≥ 0 } :
Let G = ( { S , A } , { a } , S , { r 1 , r 2 , r 3 } ) , where
r 1 = ( S → A A , { r 1 } , { r 2 } ) r 2 = ( A → S , { r 2 } , { r 1 , r 3 } ) r 3 = ( S → a , { r 3 } , ∅ ) The derivation for the string aaaa is as follows:
S ⇒ r 1 A A ⇒ r 1 A A ⇒ r 2 S A ⇒ r 2 S S ⇒ r 2 S S ⇒ r 1 A A S ⇒ r 1 A A A A ⇒ r 1 A A A A ⇒ r 2 S A A A ⇒ r 2 S S A A ⇒ r 2 S S S A ⇒ r 2 S S S S ⇒ r 2 S S S S ⇒ r 3 a S S S ⇒ r 3 a a S S ⇒ r 3 a a a S ⇒ r 3 a a a a ⇒ r 3 a a a a As can be seen from the derivation and the rules, each time r 1 and r 2 succeed, they feed back to themselves, which forces each rule to continue to rewrite the string over and over until it can do so no more. Upon failing, the derivation can switch to a different rule. In the case of r 1 , that means rewriting all Ss as AAs, then switching to r 2 . In the case of r 2 , it means rewriting all As as Ss, then switching either to r 1 , which will lead to doubling the number of Ss produced, or to r 3 which converts the Ss to as then halts the derivation. Each cycle through r 1 then r 2 therefore either doubles the initial number of Ss, or converts the Ss to as. The trivial case of generating a, in case it is difficult to see, simply involves vacuously applying r 1 , thus jumping straight to r 2 which also vacuously applies, then jumping to r 3 which produces a.
Unlike grammars controlled by prescribed sequences of production rules, which constrain the space of valid derivations but do not constrain the sorts of sentences that a production rule can apply to, grammars controlled by context conditions have no sequence constraints, but permit constraints of varying complexity on the sentences to which a production rule applies. Similar to grammars controlled by prescribed sequences, there are multiple different kinds of grammars controlled by context conditions: conditional grammars, semi-conditional grammars, random context grammars, and ordered grammars.
Conditional grammars are the simplest version of grammars controlled by context conditions. The structure of a conditional grammar is very similar to that of a normal rewrite grammar: G = ( N , T , S , P ) , where N, T, and S are as defined in a context-free grammar, and P is a set of pairs of the form ( p , R ) where p is a production rule (usually context-free), and R is a language (usually regular) over N ∪ T . When R is regular, R can just be expressed as a regular expression.
With this definition of a conditional grammar, we can define the derives relation as follows:
Given two strings x , y ∈ ( N ∪ T ) ∗ , and some production rule p = ( A → w , R ) ∈ P ,
x ⇒ p y if and only if
x = x ′ A x ″ ,
y = x ′ w x ″ , and
x ∈ R Informally then, the production rule for some pair in P can apply only to strings that are in its context language. Thus, for example, if we had some pair ( S → x , a ∗ S b ∗ ) , we can only apply this to strings consisting of any number of as followed by exactly only S followed by any number of bs, i.e. to sentences in { a m A b n : m , n ≥ 0 } , such as the strings S, aSb, aaaS, aSbbbbbb, etc. It cannot apply to strings like xSy, aaaSxbbb, etc.
Conditional grammars can generate the context-sensitive language { a 2 n : n ≥ 0 } .
Let G = ( { S , S ′ } , { a } , { f , g , h } , S ) , where
f = ( S → A A , A ∗ S + ) g = ( A → B , B ∗ A + ) h = ( B → S , S ∗ B + ) k = ( S → a , a ∗ S + ) We can then generate the sentence aaaa with the following derivation:
S ⇒ f A A ⇒ g B A ⇒ g B B ⇒ h S B ⇒ h S S ⇒ f A A S ⇒ f A A A A ⇒ g B A A A ⇒ g B B A A ⇒ g B B B A ⇒ g B B B B ⇒ h S B B B ⇒ h S S B B ⇒ h S S S B ⇒ h S S S S ⇒ k a S S S ⇒ k a a S S ⇒ k a a a S ⇒ k a a a a A semi-conditional grammar is very similar to a conditional grammar, and technically the class of semi-conditional grammars are a subset of the conditional grammars. Rather than specifying what the whole of the string must look like for a rule to apply, semi-conditional grammars specify that a string must have as substrings all of some set of strings, and none of another set, in order for a rule to apply. Formally, then, a semi-conditional grammar is a tuple G = ( N , T , S , P ) , where, N, T, and S are defined as in a CFG, and P is a set of rules like ( p , R , Q ) where p is a (usually context-free) production rule, and R and Q are finite sets of strings. The derives relation can then be defined as follows.
For two strings x A x ′ , x w x ′ ∈ ( N ∪ T ) ∗ , and some rule p = ( A → w , R , Q ) ∈ P ,
x A x ′ ⇒ p x w x ′ if and only if every string in
R is a substring of
x A x ′ , and no string in
Q is a substring of
x A x ′ The language of a semi-conditional grammar is then trivially the set of terminal strings L ( G ) = { w ∈ T ∗ : S ⇒ ∗ w } .
An example of a semi-conditional grammar is given below also as an example of random context grammars.
Random context grammars
A random context grammar is a semi-conditional grammar in which the R and Q sets are all subsets of N. Because subsets of N are finite sets over ( N ∪ T ) ∗ , it is clear that random context grammars are indeed kinds of semi-conditional grammars.
Like conditional grammars, random context grammars (and thus semi-conditional grammars) can generate the language { a 2 n : n ≥ 0 } . One grammar which can do this is:
Let G = ( { S , X , Y , A } , { a } , S , { r 1 , r 2 , r 3 , r 4 , r 5 } ) , where
r 1 = ( S → X X , ∅ , { Y , A } ) r 2 = ( X → Y , ∅ , { S } ) r 3 = ( Y → S , ∅ , { X } ) r 4 = ( S → A , ∅ , { X } ) r 5 = ( A → a , ∅ , { S } ) Consider now the production for aaaa:
S ⇒ r 1 X X ⇒ r 2 Y X ⇒ r 2 Y Y ⇒ r 3 S Y ⇒ r 3 S S ⇒ r 1 X X S ⇒ r 1 X X X X ⇒ r 2 Y X X X ⇒ r 2 Y Y X X ⇒ r 2 Y Y Y X ⇒ r 2 Y Y Y Y ⇒ r 3 S Y Y Y ⇒ r 3 S S Y Y ⇒ r 3 S S S Y ⇒ r 3 S S S S ⇒ r 4 A S S S ⇒ r 4 A A S S ⇒ r 4 A A A S ⇒ r 4 A A A A ⇒ r 5 a A A A ⇒ r 5 a a A A ⇒ r 5 a a a A ⇒ r 5 a a a a The behavior of the R sets here is trivial: any string can be rewritten according to them, because they do not require any substrings to be present. The behavior of the Q sets, however, are more interesting. In r 1 , we are forced by the Q set to rewrite an S, thus beginning an S-doubling process, only when no Ys or As are present in the string, which means only when a prior S-doubling process has been fully initiated, eliminating the possibility of only doubling some of the Ss. In r 2 , which moves the S-doubling process into its second stage, we cannot begin this process until the first stage is complete and there are no more Ss to try to double, because the Q set prevents the rule from applying if there is an S symbol still in the string. In r 3 , we complete the doubling stage by introducing the Ss back only when there are no more Xs to rewrite, thus when the second stage is complete. We can cycle through these stages as many times as we want, rewriting all Ss to XXs before then rewriting each X to a Y, and then each Y to an S, finally ending by replacing each S with an A and then an a. Because the rule for replacing S with A prohibits application to a string with an X in it, we cannot apply this in the middle of the first stage of the S-doubling process, thus again preventing us from only doubling some Ss.
Ordered grammars are perhaps one of the simpler extensions of grammars into the controlled grammar domain. An ordered grammar is simply a tuple G = ( N , T , S , P ) where N, T, and S are identical to those in a CFG, and P is a set of context-free rewrite rules with a partial ordering < . The partial ordering is then used to determine which rule to apply to a string, when multiple rules are applicable. The derives relation is then:
Given some strings x A x ′ , x w x ′ ∈ ( N ∪ T ) ∗ and some rule p = A → w ∈ P ,
x A x ′ ⇒ p x w x ′ if and only if there is no rule
p ′ = A → w ′ ∈ P such that
p < p ′ .
Like many other contextually controlled grammars, ordered grammars can enforce the application of rules in a particular order. Since this is the essential property of previous grammars that could generate the language { a 2 n : n ≥ 0 } , it should be no surprise that a grammar that explicitly uses rule ordering, rather than encoding it via string contexts, should similarly be able to capture that language. And as it turns out, just such an ordered grammar exists:
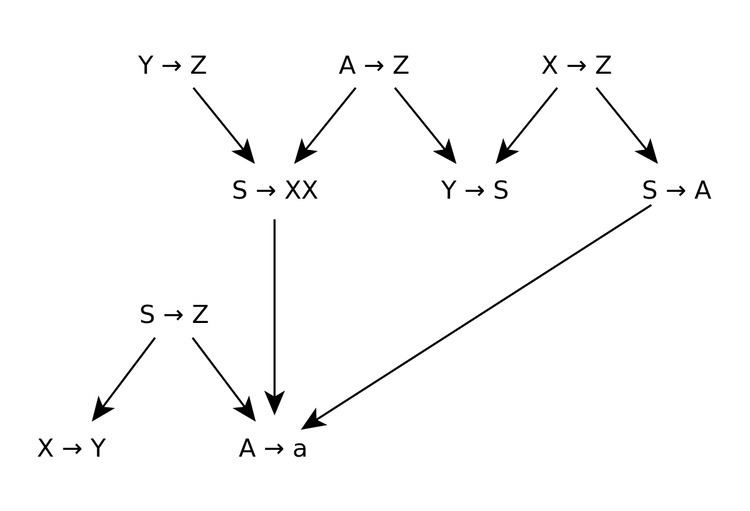
Let G = ( { S , X , Y , Z , A } , { a } , S , P ) , where P is the partially ordered set described by the Hasse diagram
The derivation for the string aaaa is simply:
S ⇒ S → X X X X ⇒ X → Y Y X ⇒ X → Y Y Y ⇒ Y → S S Y ⇒ Y → S Y Y ⇒ S → X X X X S ⇒ S → X X X X X X ⇒ X → Y Y X X X ⇒ X → Y Y Y X X ⇒ X → Y Y Y Y X ⇒ X → Y Y Y Y Y ⇒ Y → S S Y Y Y ⇒ Y → S S S Y Y ⇒ Y → S S S S Y ⇒ Y → S S S S S ⇒ S → A A S S S ⇒ S → A A A S S ⇒ S → A A A A S ⇒ S → A A A A A ⇒ A → a a A A A ⇒ A → a a a A A ⇒ A → a a a a A ⇒ A → a a a a a At each step of the way, the derivation proceeds by rewriting in cycles. Notice that if at the fifth step SY, we had four options: Y → Z , S → Z , Y → S , S → A , the first two of which halt the derivation, as Z cannot be rewritten. In the example, we used Y → S to derive SS, but consider if we had chosen S → A instead. We would have produced the string AS, the options for which are Y → Z and A → Z , both of which halt the derivation. Thus with the string SY, and conversely with YS, we must rewrite the Y to produce SS. The same hold for other combinations, so that overall, the ordering forces the derivation to halt, or else proceed by rewriting all Ss to XXs, then all Xs to Ys, then all Ys to Ss, and so on, then finally all Ss to As then all As to as. In this way, a string S n can only ever be rewritten as A n which produces as, or as S 2 n . Starting with n = 0, it should be clear that this grammar only generates the language { a 2 n : n ≥ 0 } .
A still further class of controlled grammars is the class of grammars with parallelism in the application of a rewrite operation, in which each rewrite step can (or must) rewrite more than one non-terminal simultaneously. These, too, come in several flavors: Indian parallel grammars, k-grammars, scattered context grammars, unordered scattered context grammars, and k-simple matrix grammars. Again, the variants differ in how the parallelism is defined.
An Indian parallel grammar is simply a CFG in which to use a rewrite rule, all instances of the rules non-terminal symbol must be rewritten simultaneously. Thus, for example, given the string aXbYcXd, with two instances of X, and some rule X → w , the only way to rewrite this string with this rule is to rewrite it as awbYcwd; neither awbYcXd nor aXbYcwd are valid rewrites in an Indian parallel grammar, because they did not rewrite all instances of X.
Indian parallel grammars can easily produce the language { w w : w ∈ { a , b } ∗ } :
Let G = ( { S , A } , { a , b } , S , { f , g , h , k } ) , where
f = S → A A g = A → a A h = A → b A k = A → ϵ Generating aabaab then is quite simple:
S ⇒ f A A ⇒ g a A a A ⇒ g a a A a a A ⇒ h a a b A a a b A ⇒ k a a b a a b The language { a 2 n : n ≥ 0 } is even simpler:
Let G = ( { S } , { a } , S , P ) , where P consists of
S → S S S → a It should be obvious, just from the first rule, and the requirement that all instances of a non-terminal are rewritten simultaneously with the same rule, that the number of Ss doubles on each rewrite step using the first rule, giving the derivation steps S ⇒ S 2 ⇒ S 4 ⇒ S 8 ⇒ . . . . Final application of the second rule replaces all the Ss with as, thus showing how this simple language can produce the language { a 2 n : n ≥ 0 } .
A k-grammar is yet another kind of parallel grammar, very different from an Indian parallel grammar, but still with a level of parallelism. In a k-grammar, for some number k, exactly k non-terminal symbols must be rewritten at every step (except the first step, where the only symbol in the string is the start symbol). If the string has less than k non-terminals, the derivation fails.
A 3-grammar can produce the language { a n b n c n : n ≥ 0 } , as can be seen below:
Let G = ( { S , A , B , C } , { a , b , c } , S , P ) , where P consists of:
S → A B C A → a A A → a B → b B B → b C → c C C → c With the following derivation for aaabbbccc:
S ⇒ A B C ⇒ a A b B c C ⇒ a a A b b B c c C ⇒ a a a b b b c c c At each step in the derivation except the first and last, we used the self-recursive rules A → a A , B → b B , C → c C . If we had not use the recursive rules, instead using, say, A → a , B → b B , C → c C , where one of the rules is not self-recursive, the number of non-terminals would have decreased to 2, thus making the string unable to be derived further because it would have too few non-terminals to be rewritten.
Russian parallel grammars are somewhere between Indian parallel grammars and k-grammars, defined as G = ( N , T , S , P ) , where N, T, and S are as in a context-free grammar, and P is a set of pairs ( A → w , k ) , where A → w is a context-free production rule, and k is either 1 or 2. Application of a rule p = ( A → w , k ) involves rewriting k occurrences of A to w simultaneously.
A scattered context grammar is a 4-tuple G = ( N , T , S , P ) where N, T, and S are defined as in a context-free grammar, and P is a set of tuples called matrixes p = ( A 1 → w 1 , . . . , A n → w n ) , where n > 0 can vary according to the matrix. The derives relation for such a grammar is
x ⇒ p y if and only if
p = ( A 1 → w 1 , . . . , A n → w n ) ∈ P , and
x = x 1 A 1 x 2 . . . x n A n x n + 1 , y = x 1 w 1 x 2 . . . x n w n x n + 1 , for
x i ∈ ( N ∪ T ) ∗ Intuitively, then, the matrixes in a scattered context grammar provide a list of rules which must each be applied to non-terminals in a string, where those non-terminals appear in the same linear order as the rules that rewrite them.
An unordered scattered context grammar is a scattered context grammar in which, for every rule in P, each of its permutations is also in P. As such, a rule and its permutations can instead be represented as a set rather than as tuples.
Scattered context grammars are capable of describing the language { a n b n c n : n ≥ 0 } quite easily.
Let G = ( { S , A , B , C } , { a , b , c } , S , { r 1 , r 2 , r 3 } ) , where
r 1 = ( S → A B C ) r 2 = ( A → a A , B → b B , C → c C ) r 3 = ( A → ϵ , B → ϵ , C → ϵ ) Deriving aaabbbccc then is trivial:
S ⇒ r 1 A B C ⇒ r 2 a A b B c C ⇒ r 2 a a A b b B c c C ⇒ r 2 a a a A b b b B c c c C ⇒ r 3 a a a b b b c c c