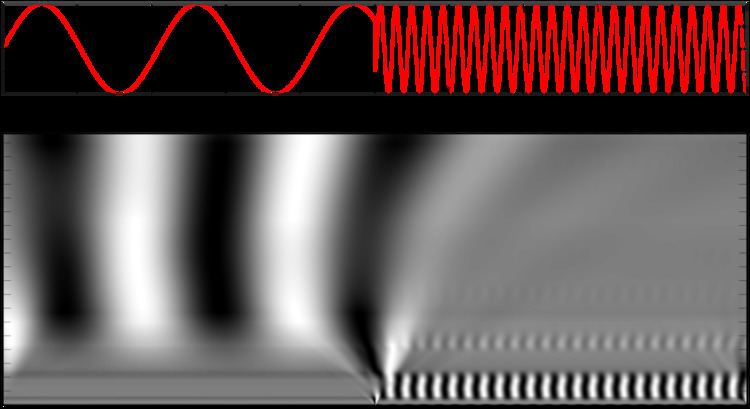
Continuous wavelet transform - Alchetron, the free social encyclopedia

In mathematics, a continuous wavelet transform (CWT) is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization. The continuous wavelet transform of a function x ( t ) at a scale (a>0) a ∈ R + ∗ and translational value b ∈ R is expressed by the following integral

where ψ ( t ) is a continuous function in both the time domain and the frequency domain called the mother wavelet and the overline represents operation of complex conjugate. The main purpose of the mother wavelet is to provide a source function to generate the daughter wavelets which are simply the translated and scaled versions of the mother wavelet. To recover the original signal x ( t ) , the first inverse continuous wavelet transform can be exploited.

x ( t ) = C ψ − 1 ∫ − ∞ ∞ ∫ − ∞ ∞ X w ( a , b ) 1 | a | 1 / 2 ψ ~ ( t − b a ) d b d a a 2

ψ ~ ( t ) is the dual function of ψ ( t ) and

C ψ = ∫ − ∞ ∞ ψ ^ ¯ ( ω ) ψ ~ ^ ( ω ) | ω | d ω

is admissible constant, where hat means Fourier transform operator. Sometimes, ψ ~ ( t ) = ψ ( t ) , then the admissible constant becomes

C ψ = ∫ − ∞ + ∞ | ψ ^ ( ω ) | 2 | ω | d ω

Traditionally, this constant is called wavelet admissible constant. A wavelet whose admissible constant satisfies

0 < C ψ < ∞

is called an admissible wavelet. An admissible wavelet implies that ψ ^ ( 0 ) = 0 , so that an admissible wavelet must integrate to zero. To recover the original signal x ( t ) , the second inverse continuous wavelet transform can be exploited.

x ( t ) = 1 2 π ψ ^ ¯ ( 1 ) ∫ − ∞ ∞ ∫ − ∞ ∞ 1 a 2 X w ( a , b ) exp ⁡ ( i t − b a ) d b d a

This inverse transform suggests that a wavelet should be defined as

ψ ( t ) = w ( t ) exp ⁡ ( i t )

where w ( t ) is a window. Such defined wavelet can be called as an analyzing wavelet, because it admits to time-frequency analysis. An analyzing wavelet is unnecessary to be admissible.

Scale factor

The scale factor a either dilates or compresses a signal. When the scale factor is relatively low, the signal is more contracted which in turn results in a more detailed resulting graph. However, the drawback is that low scale factor does not last for the entire duration of the signal. On the other hand, when the scale factor is high, the signal is stretched out which means that the resulting graph will be presented in less detail. Nevertheless, it usually lasts the entire duration of the signal.

Continuous wavelet transform properties

In definition, the continuous wavelet transform is a convolution of the input data sequence with a set of functions generated by the mother wavelet. The convolution can be computed by using a Fast Fourier Transform (FFT) algorithm. Normally, the output X w ( a , b ) is a real valued function except when the mother wavelet is complex. A complex mother wavelet will convert the continuous wavelet transform to a complex valued function. The power spectrum of the continuous wavelet transform can be represented by | X w ( a , b ) | 2 .

Applications of the wavelet transform

One of the most popular applications of wavelet transform is image compression. The advantage of using wavelet-based coding in image compression is that it provides significant improvements in picture quality at higher compression ratios over conventional techniques. Since wavelet transform has the ability to decompose complex information and patterns into elementary forms, it is commonly used in acoustics processing and pattern recognition. Moreover, wavelet transforms can be applied to the following scientific research areas: edge and corner detection, partial differential equation solving, transient detection, filter design, electrocardiogram (ECG) analysis, texture analysis, business information analysis and gait analysis.

Continuous Wavelet Transform (CWT) is very efficient in determining the damping ratio of oscillating signals (e.g. identification of damping in dynamic systems). CWT is also very resistant to the noise in the signal.

References

Continuous wavelet transform Wikipedia

(Text) CC BY-SA

Contents

Scale factor

Continuous wavelet transform properties

Applications of the wavelet transform

References