Consistent heuristic - Alchetron, The Free Social Encyclopedia

In the study of path-finding problems in artificial intelligence, a heuristic function is said to be consistent, or monotone, if its estimate is always less than or equal to the estimated distance from any neighboring vertex to the goal, plus the step cost of reaching that neighbor.

Formally, for every node N and each successor P of N, the estimated cost of reaching the goal from N is no greater than the step cost of getting to P plus the estimated cost of reaching the goal from P. That is:

h ( N ) ≤ c ( N , P ) + h ( P ) and h ( G ) = 0.

where

h is the consistent heuristic function

N is any node in the graph

P is any descendant of N

G is any goal node

c(N,P) is the cost of reaching node P from N

A consistent heuristic is also admissible, i.e. it never overestimates the cost of reaching the goal (the opposite however is not always true!). This is proved by induction on m , the length of the best path from node to goal. By assumption, h ( N m ) ≤ h ∗ ( N m ) , where h ∗ ( n ) denotes the cost of the shortest path from n to the goal. Therefore,

h ( N m + 1 ) ≤ c ( N m + 1 , N m ) + h ( N m ) ≤ c ( N m + 1 , N m ) + h ∗ ( N m ) = h ∗ ( N m + 1 ) ,

making it admissible. ( N m + 1 is any node whose best path to the goal, of length m+1, goes through some immediate child N m whose best path to the goal is of length m.)

However, an admissible heuristic h , can be made into a consistent heuristic, h ′ , through the following adjustment:

h ′ ( P ) ← max ( h ( P ) , h ( N ) − c ( N , P ) )

(Known as the pathmax equation.)

Consequences of monotonicity

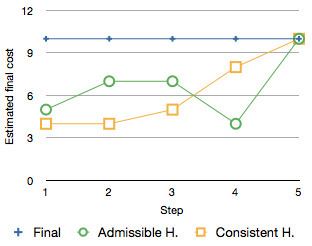
Consistent heuristics are called monotone because the estimated final cost of a partial solution, f ( N j ) = g ( N j ) + h ( N j ) is monotonically non-decreasing along the best path to the goal, where g ( N j ) = ∑ i = 2 j c ( N i − 1 , N i ) is the cost of the best path from start node N 1 to N j . It's necessary and sufficient for a heuristic to obey the triangle inequality in order to be consistent.

In the A* search algorithm, using a consistent heuristic means that once a node is expanded, the cost by which it was reached is the lowest possible, under the same conditions that Dijkstra's algorithm requires in solving the shortest path problem (no negative cost cycles). In fact, if the search graph is given cost c ′ ( N , P ) = c ( N , P ) + h ( P ) − h ( N ) for a consistent h , then A* is equivalent to best-first search on that graph using Dijkstra's algorithm. In the unusual event that an admissible heuristic is not consistent, a node will need repeated expansion every time a new best (so-far) cost is achieved for it.

References

Consistent heuristic Wikipedia

(Text) CC BY-SA