 | ||
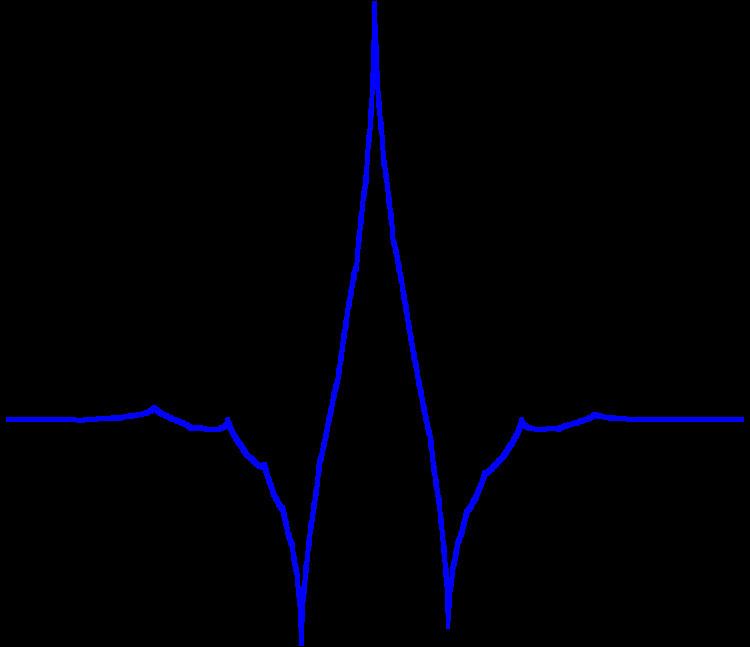
Coiflets are discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments. The wavelet is near symmetric, their wavelet functions have
Contents
Theory
Some theories about Coiflet :
Theorem 1
For a wavelet system {
and similar equivalence holds between
Theorem 2
For a wavelet system {
and similar equivalence holds between
Theorem 3
For a biorthogonal wavelet system {
for any
Coiflet coefficients
Both the scaling function (low-pass filter) and the wavelet function (High-Pass Filter) must be normalised by a factor
Mathematically, this looks like
Matlab function
F = coifwavf(W) returns the scaling filter associated with the Coiflet wavelet specified by the string W where W = 'coifN'. Possible values for N are 1, 2, 3, 4, or 5.
