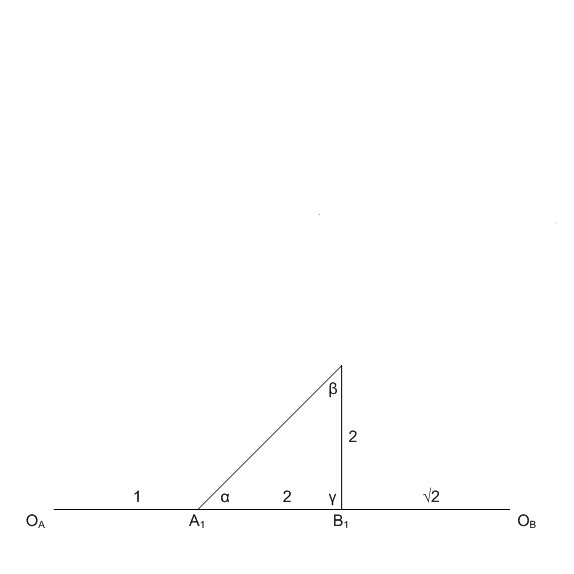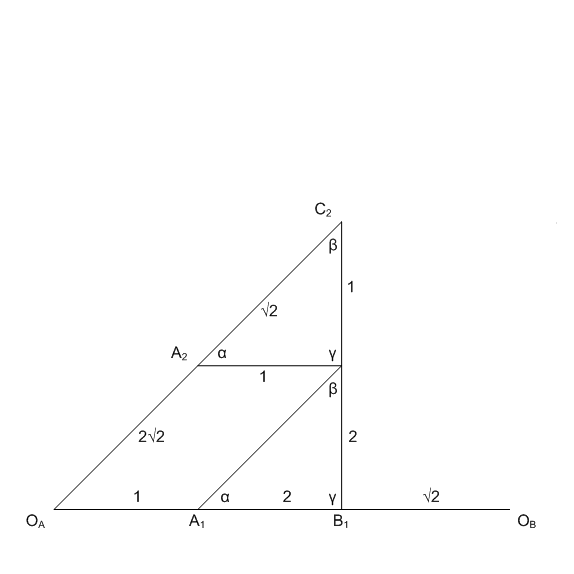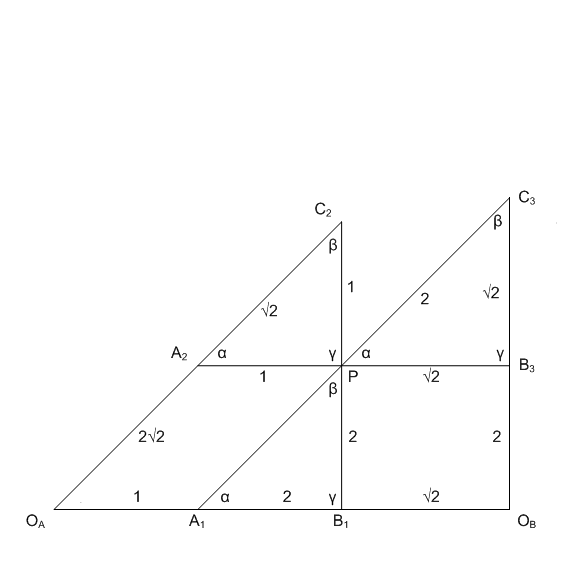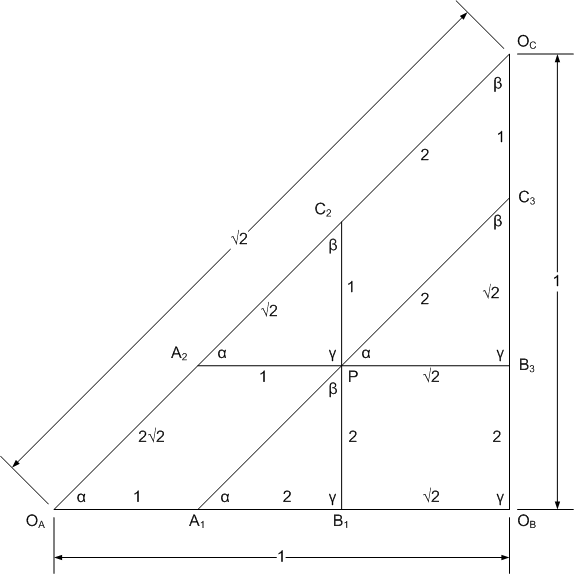 | ||
In kinematics, cognate linkages are linkages that ensure the same input-output relationship or coupler curve geometry, while being dimensionally dissimilar. In case of four-bar linkage coupler cognates, the Roberts–Chebyschev Theorem, after Samuel Roberts and Pafnuty Chebyshev, states that each coupler curve can be generated by three different four-bar linkages. These four-bar linkages can be constructed using similar triangles and parallelograms, and the Cayley diagram (named after Arthur Cayley).
Contents
Overconstrained mechanisms can be obtained by connecting two or more cognate linkages together.
Roberts–Chebyschev theorem
The theorem states for a given coupler-curve there exist three four-bar linkages, three geared five-bar linkages, and more six-bar linkages which will generate the same path. The method for generating the additional two four bar linkages from a single four-bar mechanism is described below, using the Cayley diagram.
Cayley diagram
From original triangle, ΔA1,D,B1
- Sketch Cayley diagram
- Using parallelograms, find A2 and B3 //OA,A1,D,A2 and //OB,B1,D,B3
- Using similar triangles, find C2 and C3 ΔA2,C2,D and ΔD,C3,B3
- Using a parallelogram, find OC //OC,C2,D,C3
- Check similar triangles ΔOA,OC,OB
- Separate left and right cognate
- Put dimensions on Cayley diagram
Dimensional relationships
The lengths of the four members can be found by using the law of sines. Both KL and KR are found as follows.
