 | ||
The coefficient of relationship is a measure of the degree of consanguinity (or biological relationship) between two individuals. A coefficient of inbreeding can be calculated for an individual, as a measure for the amount of pedigree collapse within that individual's genealogy. The term coefficient of relationship was defined by Sewall Wright in 1922, and was derived from his definition of the coefficient of inbreeding of 1921. The measure is most commonly used in genetics and genealogy.
Contents
In general, the higher the level of inbreeding the closer the coefficient of relationship approaches a value of 1, expressed as a percentage, and approaches a value of 0 for individuals with arbitrarily remote common ancestors.
Coefficient of inbreeding
The coefficient of inbreeding ("f") is a measure of the likelihood of genetic effects due to inbreeding to be expected based on a known pedigree (i.e. a fully documented genealogy e.g. due to a fixed system of breeding). The measure expresses the expected percentage of homozygosity arising from a given system of breeding.
For a given gene with equally common dominant and recessive variants A and a, a random-bred stock will be 50% homozygous (25% AA and 25% aa), while a closely inbred population will be 100% homozygous (100% AA or 100% aa). The coefficient of inbreeding f is thus designed to run from 0 for an expected 50% homozygosis to 1 for an expected 100% homozygosis, f=2h-1, where h is the chance of finding homozygosis in this gene.
Note that f is an expectation value for an unspecified, hypothetical, perfectly Mendelian gene. Its definition holds regardless of whether the organism's genome actually contains such a gene. Therefore, the coefficient of inbreeding is a statistical value derived from the individual's pedigree and cannot be verified or "measured" exactly by looking at the individual's genome.
The coefficient of relationship ("r") between two individuals B and C is obtained by a summation of coefficients calculated for every line by which they are connected to their common ancestors. Each such line connects the two individuals via a common ancestor, passing through no individual which is not a common ancestor more than once. A path coefficient between an ancestor A and an offspring O separated by n generations is given as:
pAO= 2−n⋅((1+fA)/(1+fO))½where fA and fO are the coefficients of inbreeding for A and O, respectively.
The coefficient of relationship rBC is now obtained by summing over all path coefficients:
rBC = Σ pAB⋅pAC.By assuming that the pedigree can be traced back to a sufficiently remote population of perfectly random-bred stock (fA=0) the definition of r may be simplified to
rBC = Σp 2−L(p),where p enumerates all paths connecting B and C with unique common ancestors (i.e. all paths terminate at a common ancestor and may not pass through a common ancestor to a common ancestor's ancestor), and L(p) is the length of the path p.
To given an (artificial) example: Assuming that two individuals share the same 32 ancestors of n=5 generations ago, but do not have any common ancestors at four or fewer generations ago, their coefficient of relationship would be
r = 2n⋅2−2n = 2−n which is, because n = 5,r = 25•2−10 = 2−5 = 1/32 which is approximately 0.0313 or 3%.Individuals for which the same situation applies for their 1024 ancestors of ten generations ago would have a coefficient of r = 2−10 = 0.1%. If follows that the value of r can be given to an accuracy of a few percent if the family tree of both individuals is known for a depth of five generations, and to an accuracy of a tenth of a percent if the known depth is at least ten generations. The contribution to r from common ancestors of 20 generations ago (corresponding to roughly 500 years in human genealogy, or the contribution from common descent from a medieval population) falls below one part-per-million.
Human relationships
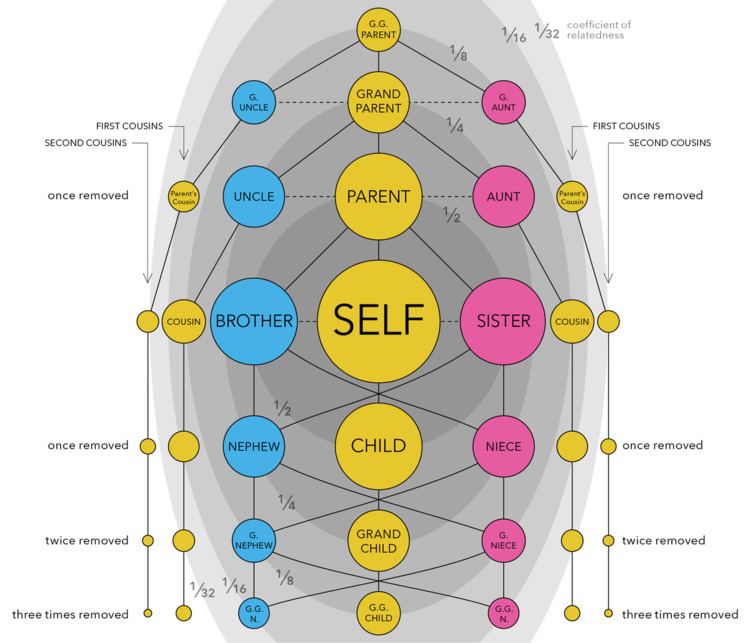
The coefficient of relationship is sometimes used to express degrees of kinship in numeric terms in human genealogy.
In human relationships, the value of the coefficient of relationship is usually calculated based on the knowledge of a full family tree extending to a comparatively small number of generations, perhaps of the order of three or four. As explained above, the value for the coefficient of relationship so calculated is thus a lower bound, with an actual value that may be up to a few percent higher. The value is accurate to within 1% if the full family tree of both individuals is known to a depth of seven generations.
Most incest laws concern the relationships where r = 25% or higher, although many ignore the rare case of double first cousins. Some jurisdictions also prohibit sexual relations or marriage between cousins of various degree, or individuals related only through adoption or affinity. Whether there is any likelihood of conception is generally considered irrelevant.
