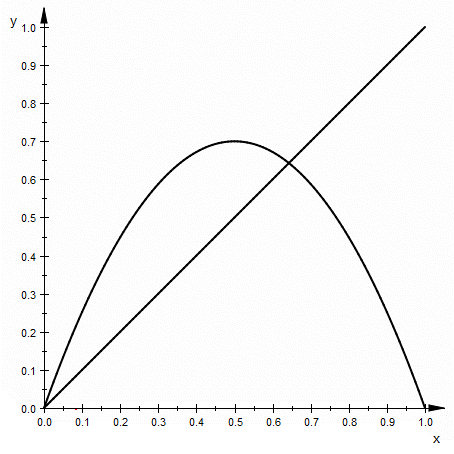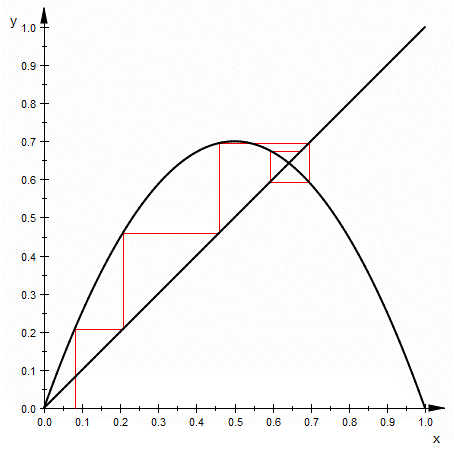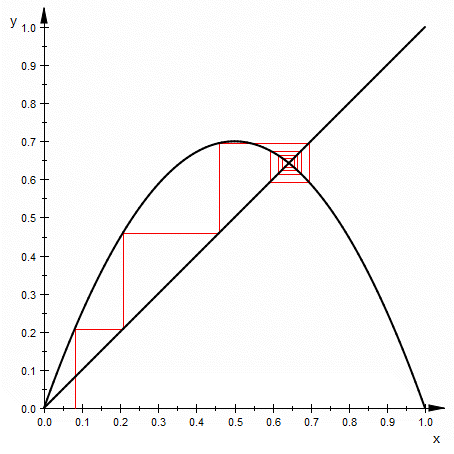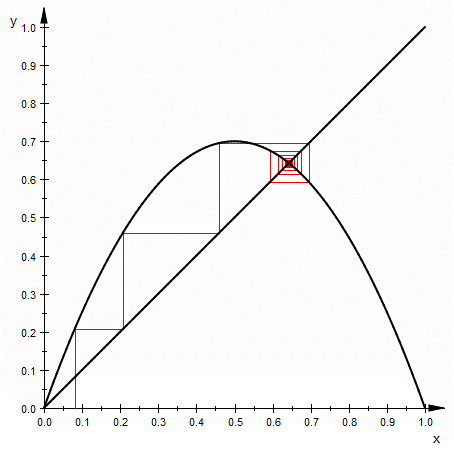 | ||
A cobweb plot, or Verhulst diagram is a visual tool used in the dynamical systems field of mathematics to investigate the qualitative behaviour of one-dimensional iterated functions, such as the logistic map. Using a cobweb plot, it is possible to infer the long term status of an initial condition under repeated application of a map.
Contents
Method
For a given iterated function f: R → R, the plot consists of a diagonal (x = y) line and a curve representing y = f(x). To plot the behaviour of a value
- Find the point on the function curve with an x-coordinate of
x 0 x 0 , f ( x 0 ) ). - Plot horizontally across from this point to the diagonal line. This has the coordinates (
f ( x 0 ) , f ( x 0 ) ). - Plot vertically from the point on the diagonal to the function curve. This has the coordinates (
f ( x 0 ) , f ( f ( x 0 ) ) ). - Repeat from step 2 as required.
Interpretation
On the cobweb plot, a stable fixed point corresponds to an inward spiral, while an unstable fixed point is an outward one. It follows from the definition of a fixed point that these spirals will center at a point where the diagonal y=x line crosses the function graph. A period 2 orbit is represented by a rectangle, while greater period cycles produce further, more complex closed loops. A chaotic orbit would show a 'filled out' area, indicating an infinite number of non-repeating values.
