Circuit minimization for Boolean functions - Alchetron, the free social encyclopedia

In Boolean algebra, circuit minimization is the problem of obtaining the smallest logic circuit (Boolean formula) that represents a given Boolean function or truth table. The unbounded circuit minimization problem was long-conjectured to be Σ 2 P -complete, a result finally proved in 2008, but there are effective heuristics such as Karnaugh maps and the Quine–McCluskey algorithm that facilitate the process.

Purpose

The problem with having a complicated circuit (i.e. one with many elements, such as logical gates) is that each element takes up physical space in its implementation and costs time and money to produce in itself. Circuit minimization may be one form of logic optimization used to reduce the area of complex logic in integrated circuits.

Example

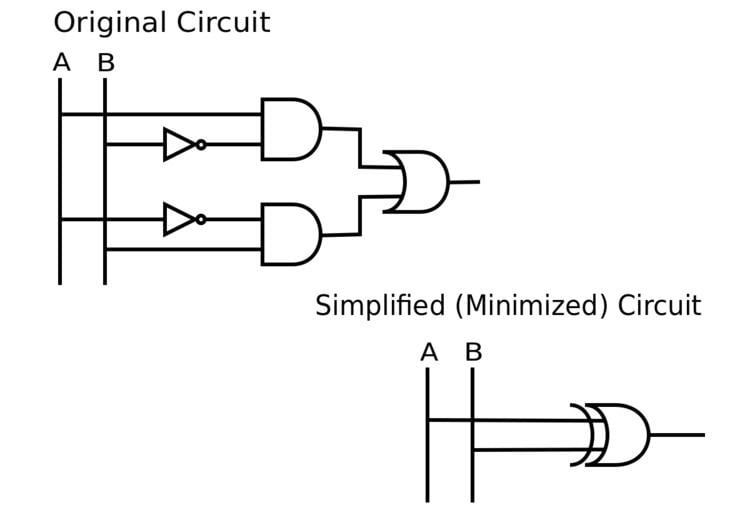
While there are many ways to minimize a circuit, this is an example that minimizes (or simplifies) a boolean function. Note that the boolean function carried out by the circuit is directly related to the algebraic expression from which the function is implemented. Consider the circuit used to represent ( A ∧ B ¯ ) ∨ ( A ¯ ∧ B ) . It is evident that two negations, two conjunctions, and a disjunction are used in this statement. This means that to build the circuit one would need two inverters, two AND gates, and an OR gate.

We can simplify (minimize) the circuit by applying logical identities or using intuition. Since the example states that A is true when B is false or the other way around, we can conclude that this simply means A ≠ B . In terms of logical gates, inequality simply means an XOR gate (exclusive or). Therefore, ( A ∧ B ¯ ) ∨ ( A ¯ ∧ B ) ⟺ A ≠ B . Then the two circuits shown below are equivalent:

You can additionally check the correctness of the result using a truth table.

References

Circuit minimization for Boolean functions Wikipedia

(Text) CC BY-SA

Contents

Purpose

Example

References