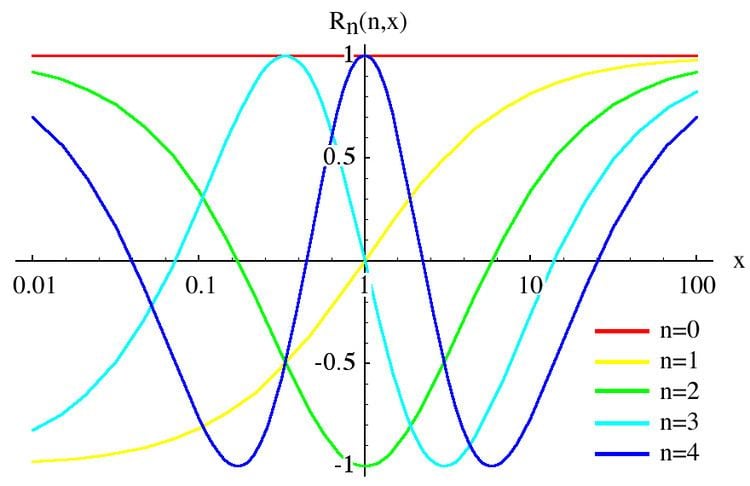
Chebyshev rational functions - Alchetron, the free social encyclopedia

In mathematics, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal. They are named after Pafnuty Chebyshev. A rational Chebyshev function of degree n is defined as:

Properties

Many properties can be derived from the properties of the Chebyshev polynomials of the first kind. Other properties are unique to the functions themselves.

Recursion

R n + 1 ( x ) = 2 x − 1 x + 1 R n ( x ) − R n − 1 ( x ) f o r n ≥ 1

Differential equations

( x + 1 ) 2 R n ( x ) = 1 n + 1 d d x R n + 1 ( x ) − 1 n − 1 d d x R n − 1 ( x ) f o r n ≥ 2 ( x + 1 ) 2 x d 2 d x 2 R n ( x ) + ( 3 x + 1 ) ( x + 1 ) 2 d d x R n ( x ) + n 2 R n ( x ) = 0

Orthogonality

Defining:

ω ( x ) = d e f 1 ( x + 1 ) x

The orthogonality of the Chebyshev rational functions may be written:

∫ 0 ∞ R m ( x ) R n ( x ) ω ( x ) d x = π c n 2 δ n m

where c n equals 2 for n = 0 and c n equals 1 for n ≥ 1 and δ n m is the Kronecker delta function.

Expansion of an arbitrary function

For an arbitrary function f ( x ) ∈ L ω 2 the orthogonality relationship can be used to expand f ( x ) :

f ( x ) = ∑ n = 0 ∞ F n R n ( x )

where

F n = 2 c n π ∫ 0 ∞ f ( x ) R n ( x ) ω ( x ) d x .

Particular values

R 0 ( x ) = 1 R 1 ( x ) = x − 1 x + 1 R 2 ( x ) = x 2 − 6 x + 1 ( x + 1 ) 2 R 3 ( x ) = x 3 − 15 x 2 + 15 x − 1 ( x + 1 ) 3 R 4 ( x ) = x 4 − 28 x 3 + 70 x 2 − 28 x + 1 ( x + 1 ) 4 R n ( x ) = 1 ( x + 1 ) n ∑ m = 0 n ( − 1 ) m ( 2 n 2 m ) x n − m

Partial fraction expansion

R n ( x ) = ∑ m = 0 n ( m ! ) 2 ( 2 m ) ! ( n + m − 1 m ) ( n m ) ( − 4 ) m ( x + 1 ) m

References

Chebyshev rational functions Wikipedia

(Text) CC BY-SA

Contents