Ceyuan haijing

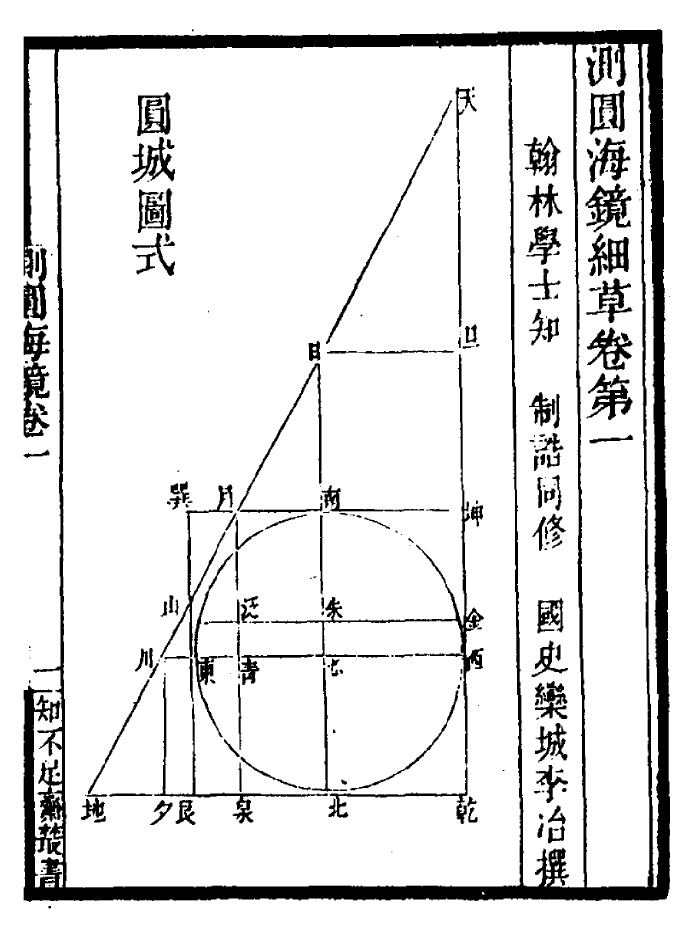
Diagram of a Round Town

The monography begins with a master diagram called the Diagram of Round Town(圆城图式). It shows a circle inscribed in a right angle triangle and four horizontal lines, four vertical lines.

TLQ, the large right angle triangle, with horizontal line LQ, vertical line TQ and hypotenuse TL

C: Center of circle:

NCS: A vertical line through C, intersect the circle and line LQ at N(南north side of city wall)， intersects south side of circle at S(南).

NCSR, Extension of line NCS to intersect hypotenuse TL at R(日)

WCE: a horizontal line passing center C, intersects circle and line TQ at W(西,west side of city wall) and circle at E(东,east side of city wall).

WCEB:extension of line WCE to intersect hypotenuse at B(川)

KSYV: a horizontal tangent at S, intersects line TQ at K(坤),hypotenuse TL at Y(月）。

HEMV: vertical tangent of circle at point E, intersects line LQ at H, hypotenuse at M(山，mountain)

HSYY,KSYV, HNQ,QSK form a square, with inscribed circle C.

Line YS, vertical line from Y intersects line LQ at S(泉， spring)

Line BJ, vertical line from point B, intersects line LQ at J(夕,night)

RD, a horizontal line from R, intersects line TQ at D(旦，day)

The North, South, East and West direction in Li Zhi's diagram are opposite to our present convention.

Triangles and their sides

There are a total of fifteen right angle triangles formed by the intersection between triangle TLQ, the four horizontal lines, and four vertical lines.

The names of these right angle triangles and their sides are summarized in the following table

In problems from Vol 2 to Vol 12, the names of these triangles are used in very terse terms. For instance

"明差","MING difference" refers to the "difference between the vertical side and horizontal side of MING triangle."叀差","ZHUANG difference" refers to the "difference between the vertical side and horizontal side of ZHUANG triangle.""明差叀差并" means "the sum of MING difference and ZHUAN difference" ( b 14 − a 14 ) + ( b 15 − a 15 )

Length of Line Segments

This section (今问正数）lists the length of line segments, the sum and difference and their combinations in the diagram of round town, given that the radius r of inscribe circle is r = 120 paces a 1 = 320 , b 1 = 640 .

The 13 segments of ith triangle(i=1 to 15) are:

1. Hypoteneuse c i
2. Horizontal a i
3. Vertical b i
4.  :勾股和 :sum of horizontal and vertical a i + b i
5.  :勾股校：difference of vertical and horizontal b i − a i
6.  :勾弦和：sum of horizontal and hypotenuse a i + c i
7.  :勾弦校：difference of hypotenuse and horizontal c i − a i
8.  :股弦和：sum of hypotenuse and vertical b i + c i
9.  :股弦校：difference of hypotenuse and vertical c i − b i
10.  :弦校和：sum of the difference and the hypotenuse c i + ( b i − a i )
11.  :弦校校：difference of the hypotenuse and the difference c i − ( b i − a i )
12.  :弦和和：sum the hypotenuse and the sum of vertical and horizontal a i + b i + c i
13.  :弦和校：difference of the sum of horizontal and vertical with the hypotenuse a i + b i

Among the fifteen right angle triangles, there are two sets of identical triangles:

ΔTRD=ΔRMZ,ΔYSG=ΔBLJ

that is

a 6 = a 7 ; b 6 = b 7 ; c 6 = c 7 ; a 8 = a 9 ; b 8 = b 9 ; c 8 = c 9 ;

Segment numbers

There are 15 x 13 =195 terms, their values are shown in Table 1:。

1. ( c 1 − a 1 ) ∗ ( c 1 ∗ b 1 ) = 1 2 * ( d 1 ) 2
2. a 10 ∗ b 11 = 1 2 ( d 1 ) 2
3. a 13 ∗ b 1 = 1 2 ( d 1 ) 2
4. a 1 ∗ b 13 = 1 2 ( d 1 ) 2
5. b 2 ∗ b 15 = ( r 1 ) 2
6. a 14 ∗ a 3 = ( r 1 ) 2
7. a 5 ∗ b 4 = ( d 1 ) 2
8. a 8 ∗ b 6 = a 9 ∗ b 7 = ( r 1 ) 2
9. ( b 14 ∗ c 14 ) ∗ ( a 15 + c 15 ) = ( r 1 ) 2
10. c 6 ∗ c 8 = c 7 ∗ c 9 ) = a 13 ∗ b 13

The Five Sums and The Five Differences

1. a 2 + b 2 + c 2 = b 1 + c 1
2. a 3 + b 3 + c 3 = a 1 + c 1
3. a 4 + b 4 + c 4 = 2 b 1
4. a 5 + b 5 + c 5 = 2 a 1
5. a 6 + b 6 + c 6 = b 1
6. a 7 + b 7 + c 7 = b 1
7. a 8 + b 8 + c 8 = a 1
8. a 9 + b 9 + c 9 = a 1
9. a 10 + b 10 + c 10 = b 1 + c 1 − a 1
10. a 11 + b 11 + c 11 = c 1 − b 1 + a 1
11. a 12 + b 12 + c 12 = c 1
12. a 13 + b 13 + c 13 = a 1 + b 1 − c 1
13. a 14 + b 14 + c 14 = c 1 − a 1
14. a 15 + b 15 + c 15 = c 1 − c 1

( b 7 − a 7 ) + ( b 8 − a 8 ) + ( b 14 − a 14 ) + ( b 15 − a 15 ) = 2 ∗ ( b 12 − a 12 )

a 8 + ( b 7 − a 7 ) + ( b 8 − a 8 ) = b 7

……………………Etc.

Li Zhi derived a total of 692 formula in Ceyuan haijing. Eight of the formula are incorrect, the rest are all correct

From vol 2 to vol 12, there are 170 problems, each problem utilizing a selected few from these formula to form 2nd order to 6th order polynomial equations. As a matter of fact, there are 21 problems yielding third order polynomial equation, 13 problem yielding 4th order polynomial equation and one problem yielding 6th order polynomial

Volume 2

This volume begins with a general hypothesis

All subsequent 170 problems are about given several segments, or their sum or difference, to find the radius or diameter of the round town. All problems follow more or less the same format; it begins with a Question, followed by description of algorithm, occasionally followed by step by step description of the procedure.

Nine types of inscribed circle

The first ten problems were solved without the use of Tian yuan shu. These problems are related to various types of inscribed circle.

Question 1

Two men A and B start from corner Q. A walks eastward 320 paces and stands still. B walks southward 600 paces and see B. What is the diameter of the circular city ?Answer: the diameter of the round town is 240 paces.This is inscribed circle problem associated with ΔTLQAlgorithm: d = 2 a 1 × b 1 a 1 + b 1 + c 1 = 2 ∗ 320 ∗ 600 320 + 600 + ( 320 2 + 600 2 ) = 240

Question 2

Two men A and B start from West gate. B walks eastward 256 paces, A walks south 480 paces and sees B. What is the diameter of the town ?Answer 240 pacesThis is inscribed circle problem associated with ΔTWBFrom Table 1, 256 = a 2 ; 480 = b 2 Algorithm: 2 a 2 × b 2 a 2 + b 2 + c 2 = d = 2 ∗ 256 ∗ 480 256 + 600 + ( 256 + 600 2 ) = 240

Question 3

inscribed circle problem associated with ΔRDN

2 a 3 × b 3 a 3 + b 3 + c 3 = d

Question 4：inscribed circle problem associated with ΔRSC

2 a 12 × b 12 c 12 = d

Question 5：inscribed circle problem associated with ΔTWB

2 a × b a + b = d

Question 6

2 a 10 × b 10 b 10 − a 10 + c 10 = d

Question 7

2 a 11 × b 11 b 11 − a 11 + c 11 = d

Question 8

2 a 13 × b 13 b 13 + a 13 − c 13 = d

Question 9

2 a 14 × b 14 c 14 − a 14 = d

Question 10

2 a 15 × b 15 c 15 − b 15 = d

Tian yuan shu

From problem 14 onwards, Li Zhi introduced "Tian yuan one" as unknown variable, and set up two expressions according to Section Definition and formula, then equate these two tian yuan shu expressions. He then solved the problem and obtained the answer.Question 14:"Suppose a man walking out from West gate and heading south for 480 paces and encountered a tree. He then walked out from the North gate heading east for 200 paces and saw the same tree. What is the radius of the round own?"。Algorithm: Set up the radius as Tian yuan one, place the counting rods representing southward 480 paces on the floor, subtract the tian yuan radius to obtain

： 480 − x

Then subtract tian yuan from eastward paces 200 to obtain:

200 − x

multiply these two expressions to get： x 2 − 680 x + 96000

that is x 2 − 680 x + 96000 = 2 x 2

thus： − x 2 − 680 x + 96000 = 0

Solve the equation and obtain r = 120

Volume 3

17 problems associated with segment b 2 i.e TW in ΔTWB

The a 10 pairs with b 11 , a 11 pairs with b 10 and a 15 pairs with b 14 in problems with same number of volume 4. In other words, for example, change a 11 of problem 2 in vol 3 into b 10 turns it into problem 2 of Vol 4.

Volume 4

17 problems, given a 3 and a second segment, find diameter of circular city.

。

Volume 5

18 problems, given b 1 。

Volume 6

18 problems.

Q1-11，13-19 given a 1 ，and a second line segment, find diameter d.Q12：given a 1 + c 3 and another line segment, find diameter d.

Volume 7

18 problems, given two line segments find the diameter of round town

Volume 8

17 problems, given three to eight segments or their sum or difference, find diameter of round city.

Problem 14

Given the sum of GAO difference and MING difference is 161 paces and the sum of MING difference and ZHUAN difference is 77 paces. What is the diameter of the round city?Answer: 120 paces.

Algorithm:

Given

( b 7 − a 7 ) + ( b 8 − a 8 ) = 161 ( b 14 − a 14 ) + ( b 15 − a 15 ) = 77

：Add these two items, and divide by 2; according to #Definitions and formula, this equals to HUANGJI difference:

( b 7 − a 7 ) + ( b 8 − a 8 ) + ( b 14 − a 14 ) + ( b 15 − a 15 ) 2 = ( b 12 − a 12 ) b 12 − a 12 = 161 + 77 2 = 119 Let Tian yuan one as the horizontal of SHANGPING (SG): x = a 8 x + 161 = x + ( b 7 − a 7 ) + ( b 8 − a 8 ) = a 8 + ( b 7 − a 7 ) + ( b 8 − a 8 ) Since a 8 + b 7 = c 12 (Definition and formula) c 12 = x + b 7 = 2 ∗ x + ( b 7 − a 7 ) + ( b 8 − a 8 ) = 2 ∗ x + 161 c 12 2 = ( x + b 7 ) 2 = ( 2 ∗ x + 161 ) 2 = 4 ∗ x 2 + 644 ∗ x + 25921 c 12 2 − ( b 12 − a 12 ) 2 = 4 ∗ x 2 + 644 ∗ x + 25921 − ( ( b 7 − a 7 ) + ( b 8 − a 8 ) + ( b 14 − a 14 ) + ( b 15 − a 15 ) ) 2 4 = 4 ∗ x 2 + 644 ∗ x + 11760 = d (diameter of round town), d 2 = ( 4 ∗ x 2 + 644 ∗ x + 11760 ) 2 = 16 ∗ x 4 + 5152 ∗ x 3 + 508816 ∗ x 2 + 15146880 ∗ x + 138297600 Now, multiply the length of RZ by 4 ∗ x 4 ∗ x ∗ b 7 = 4 ∗ x ∗ ( x + ( b 7 − a 7 ) + ( b 8 − a 8 ) ) = 4 ∗ x ∗ ( x + 161 ) = 4 ∗ x 2 + 644 ∗ x multiply it with the square of RS: d 2 = 4 ∗ x ∗ b 7 ∗ c 12 2 = ( 4 ∗ x 2 + 644 ∗ x ) ∗ ( 4 ∗ x 2 + 644 ∗ x + 25921 ) = 16 ∗ x 4 + 5152 ∗ x 3 + 518420 ∗ x 2 + 16693124 equate the expressions for the two d 2 thus 16 ∗ x 4 + 5152 ∗ x 3 + 518420 ∗ x 2 + 16693124 = 16 ∗ x 4 + 5152 ∗ x 3 + 508816 ∗ x 2 + 15146880 ∗ x + 138297600 We obtain:

9604 ∗ x 2 + 1546244 ∗ x − 138297600 = 0

solve it and we obtain x = a 8 = 64 ;

This matches the horizontal of SHANGPING 8th triangle in #Segment numbers.

Volume 9

Part I

Part II

Volume 10

8 problems

Volume 11

：Miscellaneous 18 problems：

Volume 12

14 problems on fractions

Research

In 1913, French mathematician L. van Hoe wrote an article about Ceyuan haijing. In 1982, K. Chema Ph.D thesis Etude du Livre Reflects des Mesuers du Cercle sur la mer de Li Ye. 1983, University of Singapore Mathematics Professor Lam Lay Yong: Chinese Polynomial Equations in the Thirteenth Century。