Rahul Sharma (Editor)

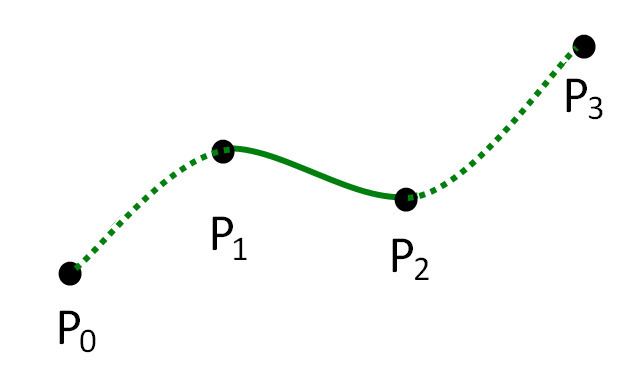
Centripetal Catmull–Rom spline

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Centripetal Catmull–Rom spline

In computer graphics, centripetal Catmull–Rom spline is a variant form of Catmull-Rom spline formulated by Edwin Catmull and Raphael Rom according to the work of Barry and Goldman. It is a type of interpolating spline (a curve that goes through its control points) defined by four control points P 0 , P 1 , P 2 , P 3 , with the curve drawn only from P 1 to P 2 .

Contents

Definition

Let P i = [ x i y i ] T denote a point. For a curve segment C defined by points P 0 , P 1 , P 2 , P 3 and knot sequence t 0 , t 1 , t 2 , t 3 , the centripetal Catmull-Rom spline can be produced by:

C = t 2 − t t 2 − t 1 B 1 + t − t 1 t 2 − t 1 B 2

where

B 1 = t 2 − t t 2 − t 0 A 1 + t − t 0 t 2 − t 0 A 2 B 2 = t 3 − t t 3 − t 1 A 2 + t − t 1 t 3 − t 1 A 3 A 1 = t 1 − t t 1 − t 0 P 0 + t − t 0 t 1 − t 0 P 1 A 2 = t 2 − t t 2 − t 1 P 1 + t − t 1 t 2 − t 1 P 2 A 3 = t 3 − t t 3 − t 2 P 2 + t − t 2 t 3 − t 2 P 3

and

t i + 1 = [ ( x i + 1 − x i ) 2 + ( y i + 1 − y i ) 2 ] α + t i

in which α ranges from 0 to 1 for knot parameterization, and i = 0 , 1 , 2 , 3 with t 0 = 0 . For centripetal Catmull-Rom spline, the value of α is 0.5 . When α = 0 , the resulting curve is the standard Catmull-Rom spline (uniform Catmull-Rom spline); when α = 1 , the product is a chordal Catmull-Rom spline.

Plugging t = t 1 into the spline equations A 1 , A 2 , A 3 , B 1 , B 2 , and C shows that the value of the spline curve at t 1 is C = P 1 . Similarly, substituting t = t 2 into the spline equations shows that C = P 2 at t 2 . This is true independent of the value of α since the equation for t i + 1 is not needed to calculate the value of C at points t 1 and t 2 .

Advantages

Centripetal Catmull–Rom spline has several desirable mathematical properties compared to the original and the other types of Catmull-Rom formulation. First, it will not form loop or self-intersection within a curve segment. Second, cusp will never occur within a curve segment. Third, it follows the control points more tightly.

Other uses

In computer vision, centripetal Catmull-Rom spline has been used to formulate an active model for segmentation. The method is termed active spline model. The model is devised on the basis of active shape model, but uses centripetal Catmull-Rom spline to join two successive points (active shape model uses simple straight line), so that the total number of points necessary to depict a shape is less. The use of centripetal Catmull-Rom spline makes the training of a shape model much simpler, and it enables a better way to edit a contour after segmentation.

Code example

The following is an implementation of the Catmull–Rom spline in Python.

UNITY C# IMPLEMENTATION

Note: If you need to implement it in 3d space with Vector3 points, just extend the float a in function GetT to this : Mathf.Pow((p1.x-p0.x), 2.0f) + Mathf.Pow((p1.y-p0.y), 2.0f) + Mathf.Pow((p1.z-p0.z), 2.0f); and convert all your Vectors2 to Vectors3.

References

Centripetal Catmull–Rom spline Wikipedia
(Text) CC BY-SA