 | ||
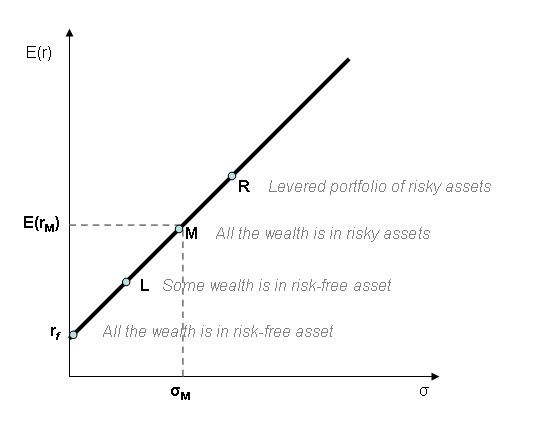
Capital market line (CML) is the tangent line drawn from the point of the risk-free asset to the feasible region for risky assets. The tangency point M represents the market portfolio, so named since all rational investors (minimum variance criterion) should hold their risky assets in the same proportions as their weights in the market portfolio.
Contents
Formula
The CML results from the combination of the market portfolio and the risk-free asset (the point L). All points along the CML have superior risk-return profiles to any portfolio on the efficient frontier, with the exception of the Market Portfolio, the point on the efficient frontier to which the CML is the tangent. From a CML perspective, the portfolio M is composed entirely of the risky asset, the market, and has no holding of the risk free asset, i.e., money is neither invested in, nor borrowed from the money market account. Points to the left of and above the CML are infeasible, whereas points to the right/below are attainable but inefficient.
Addition of leverage (the point R) creates levered portfolios that are also on the CML.
Capital market line, Sharpe ratio and alpha
All of the portfolios on the CML have the same Sharpe ratio as that of the market portfolio, i.e.
In fact, the slope of the CML is the Sharpe ratio of the market portfolio.
A stock picking rule of thumb is to buy assets whose Sharpe ratio will be above the CML and sell those whose Sharpe ratio will be below. Indeed, from the efficient market hypothesis it follows that it's impossible to beat the market. Therefore, all portfolios should have a Sharpe ratio less than or equal to the market's. In consequence, if there is a portfolio (or asset) whose Sharpe ratio will be bigger than the market's then this portfolio (or asset) has a higher return per unit of risk (i.e. the volatility
This abnormal extra return over the market's return at a given level of risk is what is called the alpha.
