Puneet Varma (Editor)

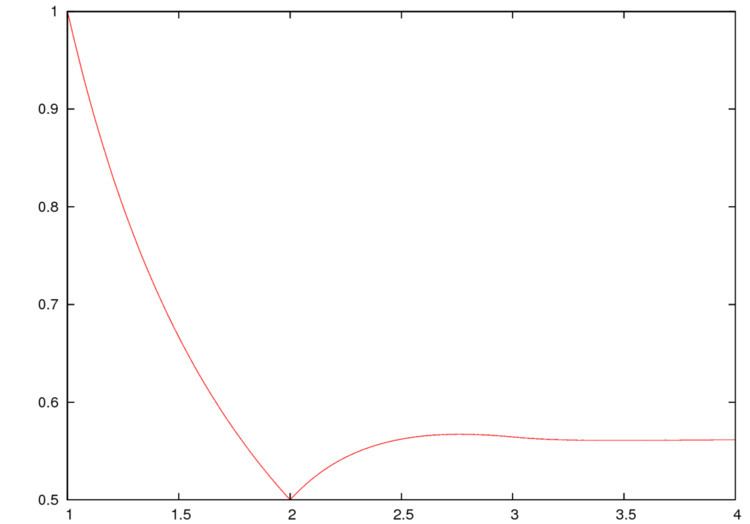
Buchstab function

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Buchstab function

The Buchstab function (or Buchstab's function) is the unique continuous function ω : R ≥ 1 → R > 0 defined by the delay differential equation

Contents

ω ( u ) = 1 u , 1 ≤ u ≤ 2 , d d u ( u ω ( u ) ) = ω ( u − 1 ) , u ≥ 2.

In the second equation, the derivative at u = 2 should be taken as u approaches 2 from the right. It is named after Alexander Buchstab, who wrote about it in 1937.

Asymptotics

The Buchstab function approaches e − γ rapidly as u → ∞ , where γ is the Euler–Mascheroni constant. In fact,

| ω ( u ) − e − γ | ≤ ρ ( u − 1 ) u , u ≥ 1 ,

where ρ is the Dickman function. Also, ω ( u ) − e − γ oscillates in a regular way, alternating between extrema and zeroes; the extrema alternate between positive maxima and negative minima. The interval between consecutive extrema approaches 1 as u approaches infinity, as does the interval between consecutive zeroes.

Applications

The Buchstab function is used to count rough numbers. If Φ(x, y) is the number of positive integers less than or equal to x with no prime factor less than y, then for any fixed u > 1,

Φ ( x , x 1 / u ) ∼ ω ( u ) x log ⁡ x 1 / u , x → ∞ .

References

Buchstab function Wikipedia
(Text) CC BY-SA