Name Bryson Heraclea | Role Mathematician | |
Bryson of Heraclea (Greek: Βρύσων Ἡρακλεώτης, gen.: Βρύσωνος; fl. late 5th-century BCE) was an ancient Greek mathematician and sophist who contributed to solving the problem of squaring the circle and calculating pi.
Contents
Life and work
Little is known about the life of Bryson; he came from Heraclea Pontica, and he may have been a pupil of Socrates. He is mentioned in the 13th Platonic Epistle, and Theopompus even claimed in his Attack upon Plato that Plato stole many ideas for his dialogues from Bryson of Heraclea. He is known principally from Aristotle, who criticizes his method of squaring the circle. He also upset Aristotle by asserting that obscene language does not exist. Diogenes Laërtius and the Suda refer several times to a Bryson as a teacher of various philosophers, but since some of the philosophers mentioned lived in the late 4th-century BCE, it is possible that Bryson became confused with Bryson of Achaea, who may have lived around that time.
Pi and squaring the circle
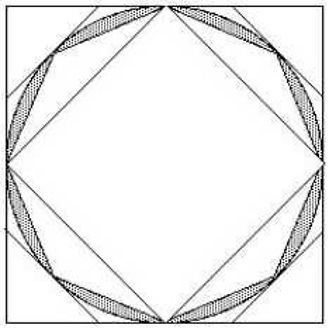
Bryson, along with his contemporary, Antiphon, was the first to inscribe a polygon inside a circle, find the polygon's area, double the number of sides of the polygon, and repeat the process, resulting in a lower bound approximation of the area of a circle. "Sooner or later (they figured), ...[there would be] so many sides that the polygon ...[would] be a circle." Bryson later followed the same procedure for polygons circumscribing a circle, resulting in an upper bound approximation of the area of a circle. With these calculations, Bryson was able to approximate π and further place lower and upper bounds on π's true value. But due to the complexity of the method, he only calculated π to a few digits. Aristotle criticized this method, but Archimedes would later use a method similar to that of Bryson and Antiphon to calculate π; however, Archimedes calculated the perimeter of a polygon instead of the area.
Robert Kilwardby on Bryson's syllogism
The 13th-century English philosopher Robert Kilwardby described Bryson's attempt of proving the quadrature of the circle as a sophistical syllogism—one which "deceives in virtue of the fact that it promises to yield a conclusion producing knowledge on the basis of specific considerations and concludes on the basis of common considerations that can produce only belief." His account of the syllogism is as follows:
