 | ||
In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.
Contents
The boxicity of a graph is the minimum dimension in which a given graph can be represented as an intersection graph of axis-parallel boxes. That is, there must exist a one-to-one correspondence between the vertices of the graph and a set of boxes, such that two boxes intersect if and only if there is an edge connecting the corresponding vertices.
Examples
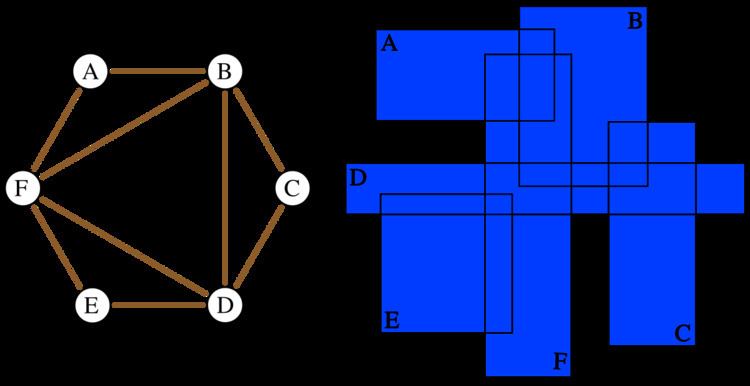
The figure shows a graph with six vertices, and a representation of this graph as an intersection graph of rectangles (two-dimensional boxes). This graph cannot be represented as an intersection graph of boxes in any lower dimension, so its boxicity is two.
Roberts (1969) showed that the graph with 2n vertices formed by removing a perfect matching from a complete graph on 2n vertices has boxicity exactly n: each pair of disconnected vertices must be represented by boxes that are separated in a different dimension than each other pair. A box representation of this graph with dimension exactly n can be found by thickening each of the 2n facets of an n-dimensional hypercube into a box. Because of these results, this graph has been called the Roberts graph, although it is better known as the cocktail party graph and it can also be understood as the Turán graph T(2n,n).
Relation to other graph classes
A graph has boxicity at most one if and only if it is an interval graph; the boxicity of an arbitrary graph G is the minimum number of interval graphs on the same set of vertices such that the intersection of the edges sets of the interval graphs is G. Every outerplanar graph has boxicity at most two, and every planar graph has boxicity at most three.
If a bipartite graph has boxicity two, it can be represented as an intersection graph of axis-parallel line segments in the plane.
Algorithmic results
Many graph problems can be solved or approximated more efficiently for graphs with bounded boxicity than they can for other graphs; for instance, the maximum clique problem can be solved in polynomial time for graphs with bounded boxicity. For some other graph problems, an efficient solution or approximation can be found if a low-dimensional box representation is known. However, finding such a representation may be difficult: it is NP-complete to test whether the boxicity of a given graph is at most some given value K, even for K = 2. Chandran, Francis & Sivadasan (2010) describe algorithms for finding representations of arbitrary graphs as intersection graphs of boxes, with a dimension that is within a logarithmic factor of the maximum degree of the graph; this result provides an upper bound on the graph's boxicity.
Despite being hard for its natural parameter, boxicity is fixed-parameter tractable when parameterized by the vertex cover number of the input graph.
