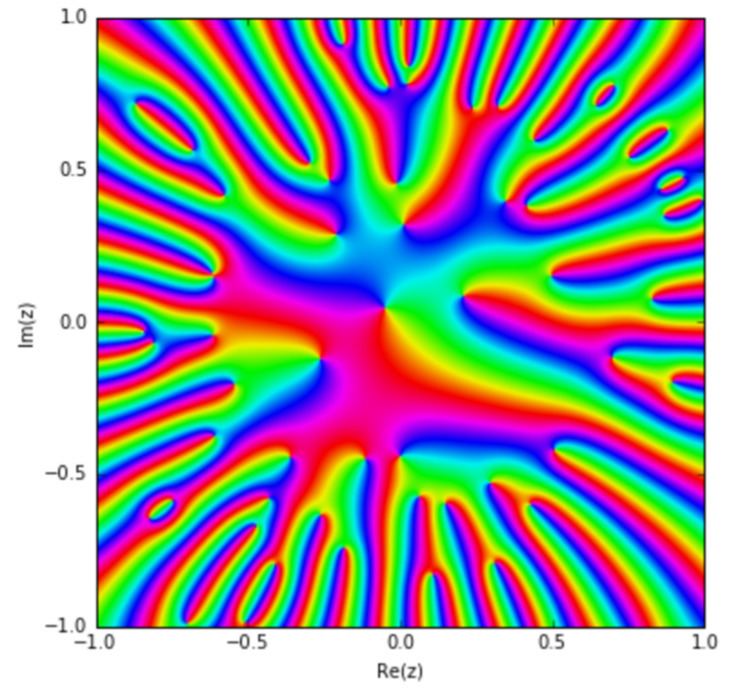
 | ||
In complex analysis, the Blaschke product is a bounded analytic function in the open unit disc constructed to have zeros at a (finite or infinite) sequence of prescribed complex numbers
Contents
a0, a1, ...inside the unit disc.
Blaschke products were introduced by Wilhelm Blaschke (1915). They are related to Hardy spaces.
Definition
A sequence of points
Given a sequence obeying the Blaschke condition, the Blaschke product is defined as
with factors
provided a ≠ 0. Here
The Blaschke product B(z) defines a function analytic in the open unit disc, and zero exactly at the an (with multiplicity counted): furthermore it is in the Hardy class
The sequence of an satisfying the convergence criterion above is sometimes called a Blaschke sequence.
Szegő theorem
A theorem of Gábor Szegő states that if f is in
Finite Blaschke products
Finite Blaschke products can be characterized (as analytic functions on the unit disc) in the following way: Assume that f is an analytic function on the open unit disc such that f can be extended to a continuous function on the closed unit disc
which maps the unit circle to itself. Then ƒ is equal to a finite Blaschke product
where ζ lies on the unit circle and mi is the multiplicity of the zero ai, |ai| < 1. In particular, if ƒ satisfies the condition above and has no zeros inside the unit circle then ƒ is constant (this fact is also a consequence of the maximum principle for harmonic functions, applied to the harmonic function log(|ƒ(z)|)).
