Binding neuron

Description of the concept

For a generic neuron the stimuli are excitatory impulses. Normally, more than single input impulse is necessary for exciting neuron up to the level when it fires and emits an output impulse. Let the neuron receives n input impulses at consecutive moments of time t 1 , t 2 , … , t n . In the BN concept the temporal coherence t c between input impulses is defined as follows

t c = 1 t n − t 1 .

The high degree of temporal coherence between input impulses suggests that in external media all n impulses can be created by a single complex event. Correspondingly, if BN is stimulated by a highly coherent set of input impulses, it fires and emits an output impulse. In the BN terminology we say that BN binds the elementary events (input impulses) into a single event (output impulse). The binding happens if the input impulses are enough coherent in time, and does not happen if those impulses do not have required degree of coherence.

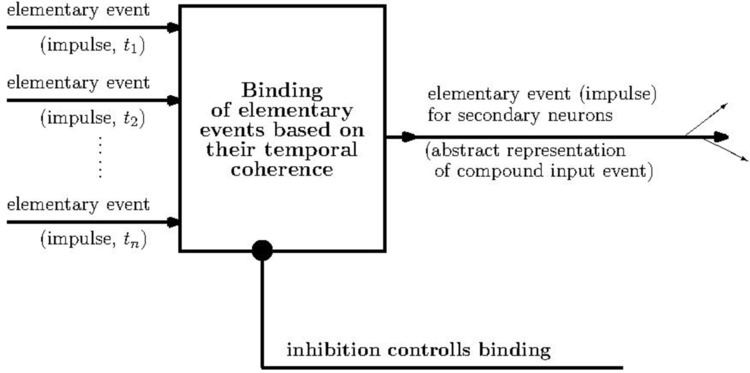
Inhibition in the BN concept (essentially, the slow somatic potassium inhibition) controls the degree of temporal coherence required for binding: the higher level of inhibition, the higher degree of temporal coherence is necessary for binding to occur.

The emitted output impulse is treated as abstract representation of the compound event (the set of coherent in time input impulses), see Scheme.

Origin

"Although a neuron requires energy, its main function is to receive signals and to send them out that is, to handle information." --- this words by Francis Crick point at the necessity to describe neuronal functioning in terms of processing of abstract signals The two abstract concepts, namely, the "coincidence detector" and "temporal integrator" are offered in this course, . The first one expects that a neuron fires a spike if a number of input impulses are received at the same time. In the temporal integrator concept a neuron fires a spike after receiving a number of input impulses distributed in time. Each of the two takes into account some features of real neurons since it is known that a realistic neuron can display both coincidence detector and temporal integrator modes of activity depending on the stimulation applied, . At the same time, it is known that a neuron together with excitatory impulses receives also inhibitory stimulation. A natural development of the two above mentioned concepts could be a concept which endows inhibition with its own signal processing role.

In the neuroscience, there is an idea of binding problem. For example, during visual perception, such features as form, color and stereopsis are represented in the brain by different neuronal assemblies. The mechanism ensuring those features to be perceived as belonging to a single real object is called "feature binding", . The experimentally approved opinion is that precise temporal coordination between neuronal impulses is required for the binding to occur, , , , , . This coordination mainly means that signals about different features must arrive to certain areas in the brain within a certain time window.

The BN concept reproduces at the level of single generic neuron the requirement, which is necessary for the feature binding to occur, and which was formulated earlier at the level of large-scale neuronal assemblies. Its formulation is made possible by the analysis of response of the Hodgkin–Huxley model to stimuli similar to those the real neurons receive in the natural conditions, see "Mathematical implementations", below.

Hodgkin–Huxley (H-H) model

Hodgkin–Huxley model — physiologically substantiated neuronal model, which operates in terms of transmembrane ionic currents, and describes mechanism of generation of action potential.

In the paper the response of the H-H model was studied numerically to stimuli U ( t ) composed of many excitatory impulses distributed randomly within a time window W :

U ( t ) = ∑ k = 1 N P V ( t − t k ) , t k ∈ [ 0 ; W ] .

Here V ( t ) denotes magnitude of excitatory postsynaptic potential at moment t ; t k — is the moment of arrival of k -th impulse; N P — is the total number of impulses the stimulus is composed of. The numbers t k are random, distributed uniformly within interval [ 0 ; W ] . The stimulating current applied in the H-H equations is as follows

I ( t ) = − C M   d U ( t ) d t ,

where C M — is the capacity of unit area of excitable membrane. The probability to generate action potential was calculated as a function of the window width W . Different constant potassium conductances were added to the H-H equations in order to create certain levels of inhibitory potential. The dependencies obtained, if recalculated as functions of T C = 1 W , which is analogous to temporal coherence of impulses in the compound stimulus, have step-like form. The location of the step is controlled by the level of inhibition potential, see Fig. 1. Due to this type of dependence, the H-H equations can be treated as mathematical model of the BN concept.

Leaky integrate and fire neuron (LIF)

Leaky integrate and fire neuron is a widely used abstract neuronal model. If to state a similar problem for the LIF neuron with appropriately chosen inhibition mechanism, then it is possible to obtain step-like dependencies similar to the Fig. 1 as well. Therefore, the LIF neuron as well can be considered as mathematical model of the BN concept.

Binding neuron model

The binding neuron model implements the BN concept in the most refined form. In this model each input impulse is stored in the neuron during fixed time τ and then disappear. This kind of memory serves as surrogate of the excitatory postsynaptic potential. The model has a threshold N t h : if the number of stored in the BN impulses exceeds N t h then the neuron fires a spike and clears it internal memory. The presence of inhibition results in the decreased τ .

In the BN model, it is necessary to control the time to live of any stored impulse during calculation of the neuron's response to input stimulation. This makes the BN model more complicated for numerical simulation than the LIF model. On the other hand, any impulse spends finite time τ in the BN model neuron. This is in contrast to the LIF model, where traces of any impulse can be present infinitely long. This property of the BN model allows to get precise description of output activity of BN stimulated with random stream of input impulses, see .

The limiting case of BN with infinite memory, τ→∞, corresponds to the temporal integrator. The limiting case of BN with infinitely short memory, τ→0, corresponds to the coincidence detector.

Integrated circuit implementation

The above-mentioned and other neuronal models and nets of them can be implemented in microchips. Among different chips it is worth mentioning the FPGA ones. The FPGA chips can be used for implementation of any neuronal model, but the BN model can be programmed most naturally because it can use only integers and do not need solving differential equations. Those features are used, e.g. in .

Limitations

As an abstract concept the BN model is subjected to necessary limitations. Among those are such as ignoring neuronal morphology, identical magnitude of input impulses, replacement of a set of transients with different relaxation times, known for a real neuron, with a single time to live, τ , of impulse in neuron, the absence of refractoriness and fast (chlorine) inhibition. The BN model has the same limitations, yet some of them can be removed in a complicated model, see, e.g. , where the BN model is used with refractorines and fast inhibition.