 | ||
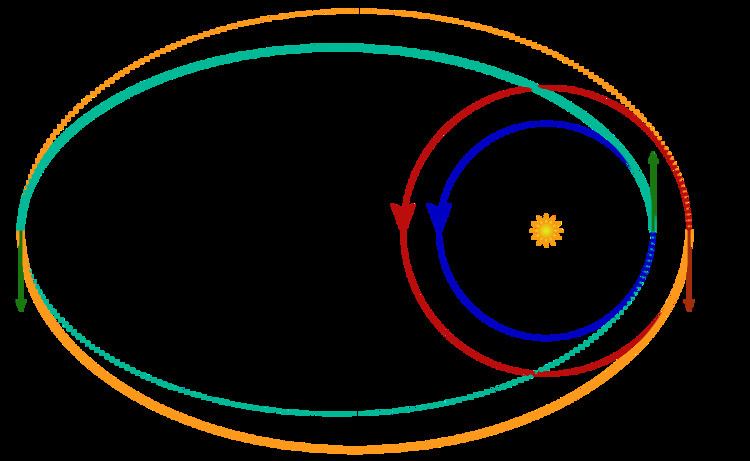
In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.
Contents
The bi-elliptic transfer consists of two half elliptic orbits. From the initial orbit, a first burn expends delta-v to boost the spacecraft into the first transfer orbit with an apoapsis at some point
While they require one more engine burn than a Hohmann transfer and generally requires a greater travel time, some bi-elliptic transfers require a lower amount of total delta-v than a Hohmann transfer when the ratio of final to initial semi-major axis is 11.94 or greater, depending on the intermediate semi-major axis chosen.
The idea of the bi-elliptical transfer trajectory was first published by Ary Sternfeld in 1934.
Delta-v
The three required changes in velocity can be obtained directly from the vis-viva equation,
where
In what follows,
Starting from the initial circular orbit with radius
When the apoapsis of the first transfer ellipse is reached at a distance
Lastly, when the final circular orbit with radius
If
The maximum savings possible can be computed by assuming that
In this case one also speaks of a bi-parabolic transfer because the two transfer trajectories no longer are ellipses but parabola. The transfer time increases to infinity too.
Transfer time
Like the Hohmann transfer, both transfer orbits used in the bi-elliptic transfer constitute exactly one half of an elliptic orbit. This means that the time required to execute each phase of the transfer is half the orbital period of each transfer ellipse.
Using the equation for the orbital period and the notation from above:
The total transfer time
And finally:
Delta-v
The figure shows the total
The thick black curve indicates the
One sees that the Hohmann transfer is always more efficient if the ratio of radii
Transfer time
The long Transfer time of the bi-elliptic transfer
is a major drawback for this maneuver. It even becomes infinite for the bi-parabolic transfer limiting case.
The Hohmann transfer takes less than half of the time because there is just one half transfer ellipse, to be precise
Example
To transfer from a circular low Earth orbit with r0=6700 km to a new circular orbit with r1=93800 km using a Hohmann transfer orbit requires a Δv of 2825.02+1308.70=4133.72 m/s. However, because r1=14r0 >11.94r0, it is possible to do better with a bi-elliptic transfer. If the spaceship first accelerated 3061.04 m/s, thus achieving an elliptic orbit with apogee at r2=40r0=268000 km, then at apogee accelerated another 608.825 m/s to a new orbit with perigee at r1=93800 km, and finally at perigee of this second transfer orbit decelerated by 447.662 m/s, entering the final circular orbit, then the total Δv would be only 4117.53 m/s, which is 16.19 m/s (0.4%) less.
The Δv saving could be further improved by increasing the intermediate apogee, at the expense of longer transfer time. For example, an apogee of 75.8r0=507,688 km (1.3 times the distance to the Moon) would result in a 1% Δv saving over a Hohmann transfer, but require a transit time of 17 days. As an impractical extreme example, an apogee of 1757r0=11,770,000 km (30 times the distance to the Moon) would result in a 2% Δv saving over a Hohmann transfer, but the transfer would require 4.5 years (and, in practice, be perturbed by the gravitational effects of other solar system bodies). For comparison, the Hohmann transfer requires 15 hours and 34 minutes.
Evidently, the bi-elliptic orbit spends more of its delta-v early on (in the first burn). This yields a higher contribution to the specific orbital energy and, due to the Oberth effect, is responsible for the net reduction in required delta-v.
