 | ||
In quantum electrodynamics, Bhabha scattering is the electron-positron scattering process:
Contents
- Differential cross section
- Mandelstam variables
- Matrix elements
- Square of matrix element
- Sum over spins
- Annihilation term s channel
- Solution
- Completeness relations
- Trace identities
- Uses
- References
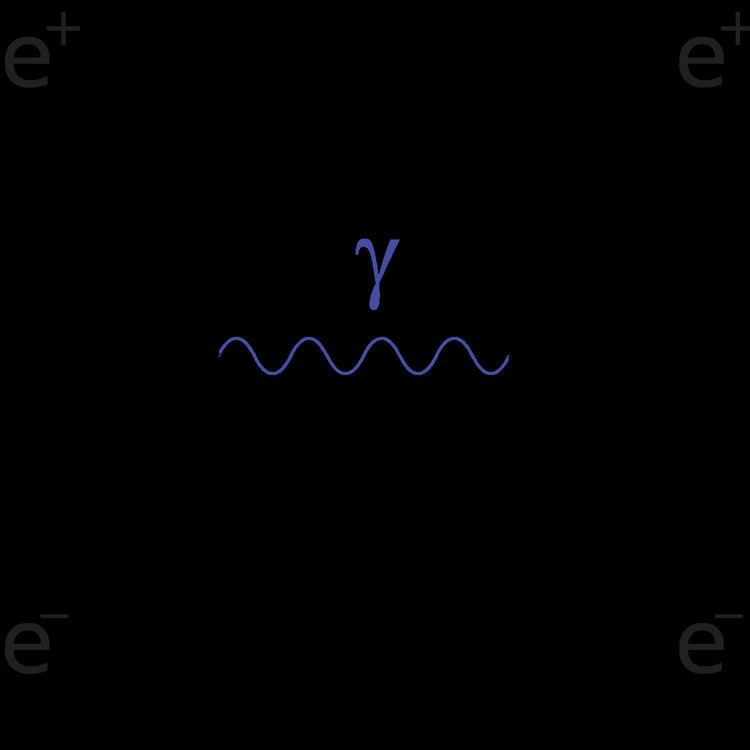
There are two leading-order Feynman diagrams contributing to this interaction: an annihilation process and a scattering process. Bhabha scattering is named after the Indian physicist Homi J. Bhabha.
The Bhabha scattering rate is used as a luminosity monitor in electron-positron colliders.
Differential cross section
To leading order, the spin-averaged differential cross section for this process is
where s,t, and u are the Mandelstam variables,
This cross section is calculated neglecting the electron mass relative to the collision energy and including only the contribution from photon exchange. This is a valid approximation at collision energies small compared to the mass scale of the Z boson, about 91 GeV; at higher energies the contribution from Z boson exchange also becomes important.
Mandelstam variables
In this article, the Mandelstam variables are defined by
where the approximations are for the high-energy (relativistic) limit.
Matrix elements
Both the scattering and annihilation diagrams contribute to the transition matrix element. By letting k and k' represent the four-momentum of the positron, while letting p and p' represent the four-momentum of the electron, and by using Feynman rules one can show the following diagrams give these matrix elements:
Notice that there is a relative sign difference between the two diagrams.
Square of matrix element
To calculate the unpolarized cross section, one must average over the spins of the incoming particles (se- and se+ possible values) and sum over the spins of the outgoing particles. That is,
First, calculate
Sum over spins
Next, we'd like to sum over spins of all four particles. Let s and s' be the spin of the electron and r and r' be the spin of the positron.
Now that is the exact form, in the case of electrons one is usually interested in energy scales that far exceed the electron mass. Neglecting the electron mass yields the simplified form:
Annihilation term (s-channel)
The process for finding the annihilation term is similar to the above. Since the two diagrams are related by crossing symmetry, and the initial and final state particles are the same, it is sufficient to permute the momenta, yielding
(This is proportional to
Solution
Evaluating the interference term along the same lines and adding the three terms yields the final result
Completeness relations
The completeness relations for the four-spinors u and v are
whereTrace identities
Main article: Trace identitiesTo simplify the trace of the Dirac gamma matrices, one must use trace identities. Three used in this article are:
- The Trace of any product of an odd number of
γ μ 's is zero -
Tr ( γ μ γ ν ) = 4 η μ ν -
Tr ( γ ρ γ μ γ σ γ ν ) = 4 ( η ρ μ η σ ν − η ρ σ η μ ν + η ρ ν η μ σ )
Using these two one finds that, for example,
Uses
Bhabha scattering has been used as a luminosity monitor in a number of e+e− collider physics experiments. The accurate measurement of luminosity is necessary for accurate measurements of cross sections.
Small-angle Bhabha scattering was used to measure the luminosity of the 1993 run of the Stanford Large Detector (SLD), with a relative uncertainty of less than 0.5%.
Electron-positron colliders operating in the region of the low-lying hadronic resonances (about 1 GeV to 10 GeV), such as the Beijing Electron Synchrotron (BES) and the Belle and BaBar "B-factory" experiments, use large-angle Bhabha scattering as a luminosity monitor. To achieve the desired precision at the 0.1% level, the experimental measurements must be compared to a theoretical calculation including next-to-leading-order radiative corrections. The high-precision measurement of the total hadronic cross section at these low energies is a crucial input into the theoretical calculation of the anomalous magnetic dipole moment of the muon, which is used to constrain supersymmetry and other models of physics beyond the Standard Model.
