 | ||
The Bethe–Salpeter equation, named after Hans Bethe and Edwin Salpeter, describes the bound states of a two-body (particles) quantum field theoretical system in a relativistically covariant formalism. The equation was actually first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation.
Contents
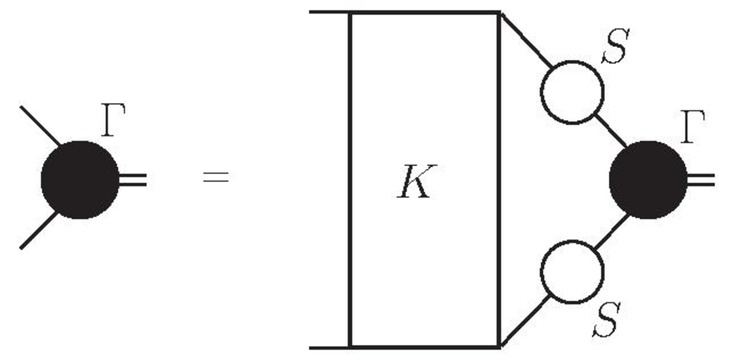
Due to its generality and its application in many branches of theoretical physics, the Bethe–Salpeter equation appears in many different forms. One form, that is quite often used in high energy physics is
where Γ is the Bethe–Salpeter amplitude, K the interaction and S the propagators of the two participating particles.
In quantum theory, bound states are objects that live for an infinite time (otherwise they are called resonances), thus the constituents interact infinitely many times. By summing up, infinitely many times, all possible interactions that can occur between the two constituents, the Bethe–Salpeter equation is a tool to calculate properties of bound states. Its solution, the Bethe–Salpeter amplitude, is a description of the bound state under consideration.
As it can be derived via identifying bound-states with poles in the S-matrix, it can be connected to the quantum theoretical description of scattering processes and Green's functions.
The Bethe–Salpeter equation is a general quantum field theoretical tool, thus applications for it can be found in any quantum field theory. Some examples are positronium (bound state of an electron–positron pair), excitons (bound state of an electron–hole pair), and mesons (as quark-antiquark bound-state).
Even for simple systems such as the positronium, the equation cannot be solved exactly although the equation can in principle be formulated exactly. Fortunately, a classification of the states can be achieved without the need for an exact solution. If one of the particles is significantly more massive than the other, the problem is considerably simplified as one solves the Dirac equation for the lighter particle under the external potential of the heavier particle.
Derivation
The starting point for the derivation of the Bethe–Salpeter equation is the two-particle (or four point) Dyson equation
in momentum space, where "G" is the two-particle Green function
where P is the total momentum of the system. One sees, that if for this momentum the equation
Comparing the residues yields
This is already the Bethe–Salpeter equation, written in terms of the Bethe–Salpeter wave functions. To obtain the above form one introduces the Bethe–Salpeter amplitudes "Γ"
and gets finally
which is written down above, with the explicit momentum dependence.
Ladder approximation
In principle the interaction kernel K contains all possible two-particle-irreducible interactions that can occur between the two constituents. Thus, in practical calculations one has to model it and only choose a subset of the interactions. As in quantum field theories, interaction is described via the exchange of particles (e.g. photons in quantum electrodynamics, or gluons in quantum chromodynamics), the most simple interaction is the exchange of only one of these force-particles.
As the Bethe–Salpeter equation sums up the interaction infinitely many times, the resulting Feynman graph has the form of a ladder.
While in Quantum electrodynamics the simplicity of the ladder approximation caused a lot of problems and thus crossed ladder terms had to be included, in Quantum chromodynamics this approximation is used quite a lot to calculate hadron masses, since it respects Chiral symmetry breaking and therefore an important part of the generation these masses.
Normalization
As for any homogeneous equation, the solution of the Bethe–Salpeter equation is determined only up to a numerical factor. This factor has to be specified by a certain normalization condition. For the Bethe–Salpeter amplitudes this is usually done by demanding probability conservation (similar to the normalization of the quantum mechanical Wave function), which corresponds to the equation
Normalizations to the charge and energy-momentum tensor of the bound state lead to the same equation. In ladder approximation the Interaction kernel does not depend on the total momentum of the Bethe–Salpeter amplitude, thus, for this case, the second term of the normalization condition vanishes.
