Bernoulli differential equation - Alchetron, the free social encyclopedia


Similar Power series solution of differential equations, Binomial differential equation, Homogeneous differential equation

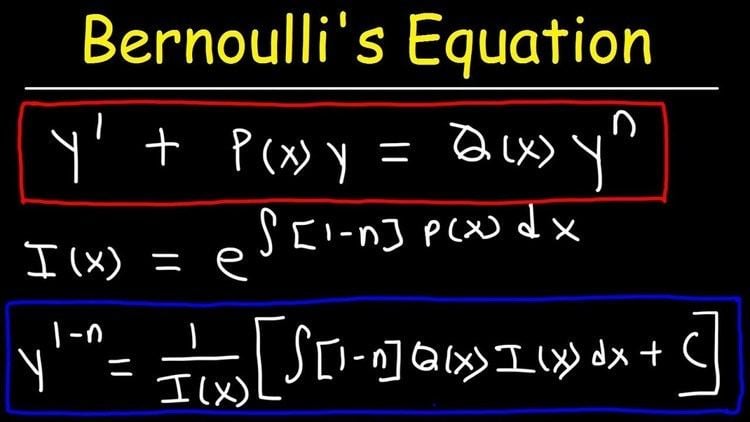
Bernoulli's Equation For Differential Equations - YouTube

In mathematics, an ordinary differential equation of the form:

is called a Bernoulli differential equation where n is any real number and n ≠ 0 or n ≠ 1 . It is named after Jacob Bernoulli who discussed it in 1695. Bernoulli equations are special because they are nonlinear differential equations with known exact solutions. A famous special case of the Bernoulli equation is the logistic differential equation.

Transformation to a linear differential equation

Note that for n = 0 and n = 1 , the Bernoulli equation is linear. For n ≠ 0 and n ≠ 1 , the substitution u = y 1 − n reduces any Bernoulli equation to a linear differential equation. For example:

Let's consider the following differential equation: x d y d x + y = x 2 y 2

Rewriting it in the Bernoulli form (with n = 2 ): d y d x + 1 x y = x y 2

Now, substituting u = y − 1 we get: d u d x − 1 x u = − x , which is a linear differential equation.

Solution

Let x 0 ∈ ( a , b ) and

{ z : ( a , b ) → ( 0 , ∞ ) , if α ∈ R ∖ { 1 , 2 } , z : ( a , b ) → R ∖ { 0 } , if α = 2 ,

be a solution of the linear differential equation

z ′ ( x ) = ( 1 − α ) P ( x ) z ( x ) + ( 1 − α ) Q ( x ) .

Then we have that y ( x ) := [ z ( x ) ] 1 1 − α is a solution of

y ′ ( x ) = P ( x ) y ( x ) + Q ( x ) y α ( x ) , y ( x 0 ) = y 0 := [ z ( x 0 ) ] 1 1 − α .

And for every such differential equation, for all α > 0 we have y ≡ 0 as solution for y 0 = 0 .

Example

Consider the Bernoulli equation (more specifically Riccati's equation).

y ′ − 2 y x = − x 2 y 2

We first notice that y = 0 is a solution. Division by y 2 yields

y ′ y − 2 − 2 x y − 1 = − x 2

Changing variables gives the equations

w = 1 y w ′ = − y ′ y 2 . − w ′ − 2 x w = − x 2 w ′ + 2 x w = x 2

which can be solved using the integrating factor

M ( x ) = e 2 ∫ 1 x d x = e 2 ln ⁡ x = x 2 .

Multiplying by M ( x ) ,

w ′ x 2 + 2 x w = x 4 ,

Note that left side is the derivative of w x 2 . Integrating both sides, with respect to x , results in the equations

∫ w ′ x 2 + 2 x w d x = ∫ x 4 d x w x 2 = 1 5 x 5 + C 1 y x 2 = 1 5 x 5 + C

The solution for y is

y = x 2 1 5 x 5 + C .

References

Bernoulli differential equation Wikipedia

(Text) CC BY-SA

Contents

Transformation to a linear differential equation

Solution

Example

References