Banach bundle

Definition of a Banach bundle

Let M be a Banach manifold of class C^p with p ≥ 0, called the base space; let E be a topological space, called the total space; let π : E → M be a surjective continuous map. Suppose that for each point x ∈ M, the fibre E_x = π⁻¹(x) has been given the structure of a Banach space. Let

{ U i | i ∈ I }

be an open cover of M. Suppose also that for each i ∈ I, there is a Banach space X_i and a map τ_i

τ i : π − 1 ( U i ) → U i × X i

such that

the map τ_i is a homeomorphism commuting with the projection onto U_i, i.e. the following diagram commutes:

and for each x ∈ U_i the induced map τ_ix on the fibre E_xis an invertible continuous linear map, i.e. an isomorphism in the category of topological vector spaces;

if U_i and U_j are two members of the open cover, then the map

is a morphism (a differentiable map of class C^p), where Lin(X; Y) denotes the space of all continuous linear maps from a topological vector space X to another topological vector space Y.

The collection {(U_i, τ_i)|i∈I} is called a trivialising covering for π : E → M, and the maps τ_i are called trivialising maps. Two trivialising coverings are said to be equivalent if their union again satisfies the two conditions above. An equivalence class of such trivialising coverings is said to determine the structure of a Banach bundle on π : E → M.

If all the spaces X_i are isomorphic as topological vector spaces, then they can be assumed all to be equal to the same space X. In this case, π : E → M is said to be a Banach bundle with fibre X. If M is a connected space then this is necessarily the case, since the set of points x ∈ M for which there is a trivialising map

τ i x : π − 1 ( x ) → X

for a given space X is both open and closed.

In the finite-dimensional case, the second condition above is implied by the first.

Examples of Banach bundles

If V is any Banach space, the tangent space T_xV to V at any point x ∈ V is isomorphic in an obvious way to V itself. The tangent bundle TV of V is then a Banach bundle with the usual projection

This bundle is "trivial" in the sense that TV admits a globally defined trivialising map: the identity function

If M is any Banach manifold, the tangent bundle TM of M forms a Banach bundle with respect to the usual projection, but it may not be trivial.

Similarly, the cotangent bundle T*M, whose fibre over a point x ∈ M is the topological dual space to the tangent space at x:

also forms a Banach bundle with respect to the usual projection onto M.

There is a connection between Bochner spaces and Banach bundles. Consider, for example, the Bochner space X = L²([0, T]; H¹(Ω)), which might arise as a useful object when studying the heat equation on a domain Ω. One might seek solutions σ ∈ X to the heat equation; for each time t, σ(t) is a function in the Sobolev space H¹(Ω). One could also think of Y = [0, T] × H¹(Ω), which as a Cartesian product also has the structure of a Banach bundle over the manifold [0, T] with fibre H¹(Ω), in which case elements/solutions σ ∈ X are cross sections of the bundle Y of some specified regularity (L², in fact). If the differential geometry of the problem in question is particularly relevant, the Banach bundle point of view might be advantageous.

Morphisms of Banach bundles

The collection of all Banach bundles can be made into a category by defining appropriate morphisms.

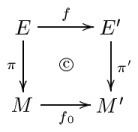
Let π : E → M and π′ : E′ → M′ be two Banach bundles. A Banach bundle morphism from the first bundle to the second consists of a pair of morphisms

f 0 : M → M ′ ; f : E → E ′ .

For f to be a morphism means simply that f is a continuous map of topological spaces. If the manifolds M and M′ are both of class C^p, then the requirement that f₀ be a morphism is the requirement that it be a p-times continuously differentiable function. These two morphisms are required to satisfy two conditions (again, the second one is redundant in the finite-dimensional case):

the diagram

commutes, and, for each x ∈ M, the induced mapis a continuous linear map;

for each x₀ ∈ M there exist trivialising maps

such that x₀ ∈ U, f₀(x₀) ∈ U′,and the mapis a morphism (a differentiable map of class C^p).

Pull-back of a Banach bundle

One can take a Banach bundle over one manifold and use the pull-back construction to define a new Banach bundle on a second manifold.

Specifically, let π : E → N be a Banach bundle and f : M → N a differentiable map (as usual, everything is C^p). Then the pull-back of π : E → N is the Banach bundle f*π : f*E → M satisfying the following properties:

for each x ∈ M, (f*E)_x = E_f(x);

there is a commutative diagram

with the top horizontal map being the identity on each fibre;

if E is trivial, i.e. equal to N × X for some Banach space X, then f*E is also trivial and equal to M × X, and

is the projection onto the first coordinate;

if V is an open subset of N and U = f⁻¹(V), then

and there is a commutative diagramwhere the maps at the "front" and "back" are the same as those in the previous diagram, and the maps from "back" to "front" are (induced by) the inclusions.