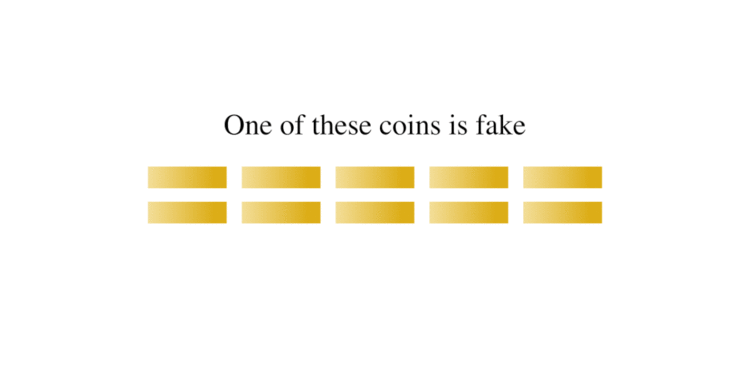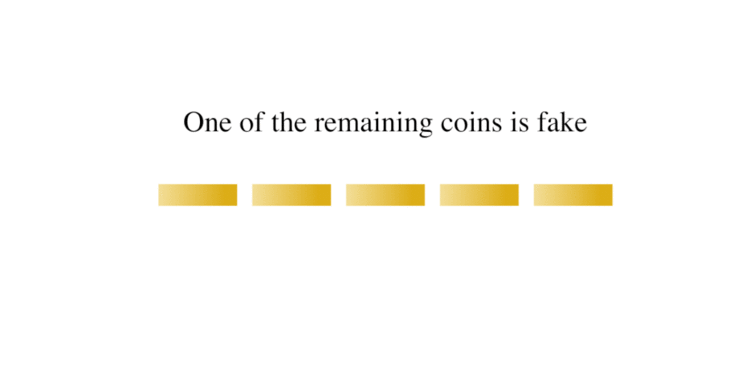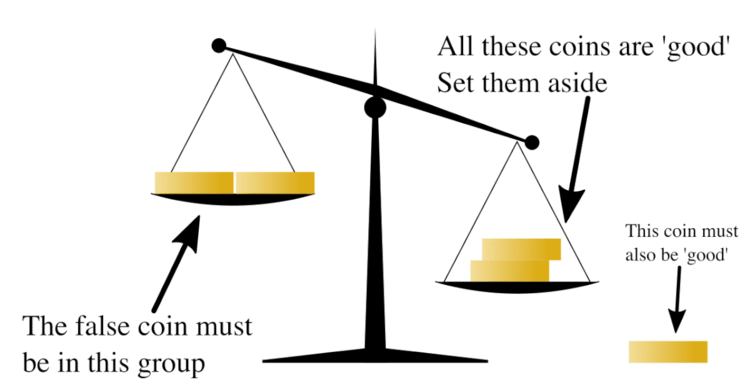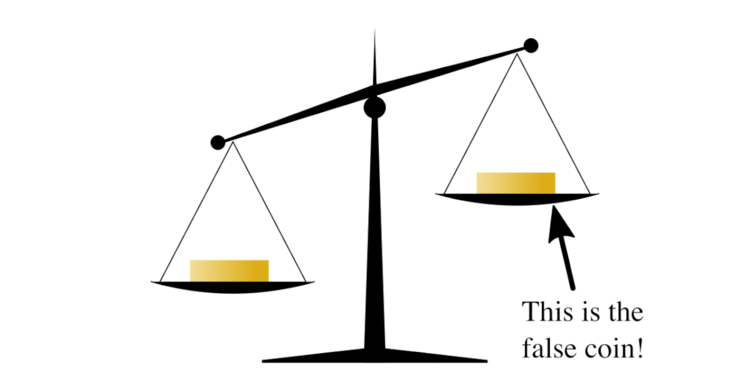Balance puzzle

The nine-coin problem

A well-known example has nine (or fewer) items, say coins (or balls), that are identical in weight save for one, which in this example is lighter than the others—a counterfeit (an oddball). The difference is only perceptible by weighing them on scale—but only the coins themselves can be weighed. Is it possible to isolate the counterfeit coin with only two weighings?

Solution

To find a solution, we first consider the maximum number of items from which one can find the lighter one in just one weighing. The maximum number possible is three. To find the lighter one we can compare any two coins, leaving the third out. If the two coins tested weigh the same, then the lighter coin must be one of those not on the balance. Otherwise, it is the one indicated as lighter by the balance.

Now, imagine the nine coins in three stacks of three coins each. In one move we can find which of the three stacks is lighter (i.e. the one containing the lighter coin). It then takes only one more move to identify the light coin from within that lighter stack. So in two weighings we can find a single light coin from a set of 3 × 3 = 9 .

By extension, it would take only three weighings to find the odd light coin among 27 coins, and four weighings to find it from 81 coins.

The twelve-coin problem

A more complex version has twelve coins, at least eleven of which are identical. If one is different, we don't know whether it is heavier or lighter than the others. This time the balance may be used three times to determine if there is a unique coin—and if there is, to isolate it and determine its weight relative to the others. (This puzzle and its solution first appeared in an article in 1945.) The problem has a simpler variant with three coins in two weighings, and a more complex variant with 39 coins in four weighings.

Solution

This problem has more than one solution. One is easily scalable to a higher number of coins by using base-three numbering: labeling each coin with a different number of three digits in base three, and positioning at the n-th weightings all the coins that are labeled with the n-th digit identical to the label of the plate (with three plates, one on each side of the scale and one off the scale). Other step-by-step procedures are similar to the following. It is less straightforward for this problem, and the second and third weightings depend on what has happened previously, although that need not be the case (see below).

Four coins are put on each side. There are two possibilities:

1. One side is heavier than the other. If this is the case, remove three coins from the heavier side, move three coins from the lighter side to the heavier side, and place three coins that were not weighed the first time on the lighter side. (Remember which coins are which.) There are three possibilities:2. Both sides are even. If this is the case, all eight coins are identical and can be set aside. Take the four remaining coins and place three on one side of the balance. Place 3 of the 8 identical coins on the other side. There are three possibilities:

With a reference coin

If there is one authentic coin for reference then the suspect coins can be thirteen. Number the coins from 1 to 13 and the authentic coin number 0 and perform these weighings in any order:

0, 1, 4, 5, 6 against 7, 10, 11, 12, 13

0, 2, 4, 10, 11 against 5, 8, 9, 12, 13

0, 3, 8, 10, 12 against 6, 7, 9, 11, 13

If the scales are only off balance once, then it must be one of the coins 1, 2, 3—which only appear in one weighing. If there is never balance then it must be one of the coins 10–13 that appear in all weighings. Picking out the one counterfeit coin corresponding to each of the 27 outcomes is always possible (13 coins one either too heavy or too light is 26 possibilities) except when all weighings are balanced, in which case there is no counterfeit coin (or its weight is correct). If coins 0 and 13 are deleted from these weighings they give one generic solution to the 12-coin problem.

If two coins are counterfeit, this procedure, in general, does not pick either of these, but rather some authentic coin. For instance, if both coins 1 and 2 are counterfeit, either coin 4 or 5 is wrongly picked.

Without a reference coin

In a relaxed variation of this puzzle, one only needs to find the counterfeit coin without necessarily being able to tell its weight relative to the others. In this case, clearly any solution that previously weighed every coin at some point can be adapted to handle one extra coin. This coin is never put on the scales, but if all weighings are balanced it is picked as the counterfeit coin. It is not possible to do any better, since any coin that is put on the scales at some point and picked as the counterfeit coin can then always be assigned weight relative to the others.

A method which weighs the same sets of coins regardless of outcomes lets one either

1. (among 12 coins A-L) conclude if they all weigh the same, or find the odd coin and tell if it is lighter or heavier, or
2. (among 13 coins A-M) find the odd coin, and, for 12 of them, tell if it is lighter or heavier.

The three possible outcomes of each weighing can be denoted by "" for the left side being lighter, "/" for the right side being lighter, and "-" for both sides having the same weight. The symbols for the weighings are listed in sequence. For example, "//-" means that the right side is lighter in the first and second weighings, and both sides weigh the same in the third weighing. Three weighings give the following 3³ = 27 outcomes. Except for "---", the sets are divided such that each set on the right has a "/" where the set on the left has a "", and vice versa:

/// // /// /// //- /--/ -//- -/- //-- -//- /-//-- ---/- ----/ -----

As each weighing gives a meaningful result only when the number of coins on the left side is equal to the number on the right side, we disregard the first row, so that each column has the same number of "" and "/" symbols (four of each). The rows are labelled, the order of the coins being irrelevant:

// A light / A heavy// B light / B heavy// C light / C heavy/- D light /- D heavy-/ E light -/ E heavy/- F light -/ F heavy- G light //- G heavy- H light -// H heavy- I light /-/ I heavy/-- J light -- J heavy-/- K light -- K heavy--/ L light -- L heavy--- M either lighter or heavier (13-coin case), or all coins weigh the same (12-coin case)

Using the pattern of outcomes above, the composition of coins for each weighing can be determined; for example the set "/- D light" implies that coin D must be on the left side in the first weighing (to cause that side to be lighter), on the right side in the second, and unused in the third:

1st weighing: left side: ADGI, right side: BCFJ2nd weighing: left side: BEGH, right side: ACDK3rd weighing: left side: CFHI, right side: ABEL

The outcomes are then read off the table. For example, if the right side is lighter in the first two weighings and both sides weigh the same in the third, the corresponding code "//- G heavy" implies that coin G is the odd one, and it is heavier than the others.

Generalizations

The generalization of this problem is described in

Let R n be the n -dimensional Euclidean space, [ e 1 , e 2 ] be the inner product of vectors e 1 and e 2 from R n , For vectors e = ( e 1 , … , e n ) ∈ R n and subsets E = { e j } ⊆ R n , the operations ( ⋅ ) ∗ and ( ⋅ ) + are defined, respectively, as e ∗ = ( s i g n ( e i ) ) i  ; E ∗ = { ( e j ) ∗ } , e + = ( | s i g n ( e i ) | ) i , E + = { ( e j ) + } . By I n we shall denote the discrete [−1; 1]-cube in R n ; i.e., the set of all sequences of length n over the alphabet I = { − 1 , 0 , 1 } The set I t n = { x ∈ I n | w ( x ) ≤ t } ⊆ I n is the discrete ball of radius t (in the Hamming metric w ( ) ) with centre at the point 0 . Relative weights of n objects are given by a vector x = ( x 1 , … , x n ) ∈ I n , which defines the configurations of weights of the objects: the i th object has standard weight if x i = 0 ; the weight of the i th object is greater (smaller) by a constant (unknown) value if x i = 1 (respectively, x i = − 1 ). The vector x + characterizes the types of objects: the standard type, the non-standard type (i.e., configurations of types), and it does not contain information about relative weights of non-standard objects.

A weighing (a check) is given by a vector h ∈ I n ; the result of a weighing for a situation x ∈ I n is s ( x ; h ) = s i g n ( [ x ; h ] ) . The weighing given by a vector h = ( h 1 , … , h n ) has the following interpretation: for a given check the i th object participates in the weighing if h i ≠ 0 ; it is put on the left balance pan if h i < 0 and is put on the right pan if h i > 0. For each weighing h , both pans should contain the same number of objects: if on some pan the number of objects is smaller than as it should be, then it receives some r ( h ) = [ h ; 1 , … , 1 ] reference objects. The result of a weighing s ( x ; h ) describes the following cases: the balance if s ( x ; h ) = 0 , the left pan outweights the right one if s ( x ; h ) = − 1 , and the right pan outweights the left one if s ( x ; h ) = 1. The incompleteness of initial information about the distribution of weights of a group of objects is characterized by the set of admissible distributions of weights of objects Z ⊆ I n , which is also called the set of admissible situations, the elements of z ∈ Z are called admissible situations.

Each weighing h induces the partition of the set I n by the plane (hyperplane ) [ x ; h ] = 0 into three parts W ( s | I ; h ) = { x ∈ I | s ( x ; h ) = s } , s ∈ I , and defines the corresponding partition of the set Z = W ( 0 | Z , h ) + W ( 1 | Z , h ) + W ( − 1 | Z , h ) , where W ( s | Z , h ) = W ( s | I , h ) ∩ Z .

Definition 1. A weighing algorithm (WA) A of length m is a sequence A =< A 1 , … , A m > , where A j : I j − 1 → I n is the function determining the check h j = A j ( s j − 1 ) ; h j ∈ I n , at each j th step, j = 1 , 2 , … , m , of the algorithm from the results of s j − 1 = ( s 1 , … , s j − 1 ) ∈ I j − 1 weighings at the previous steps ( h 1 = A 1 ( ) is a given initial check).

Let S ( Z , A ) be the set of all ( Z , A ) -syndromes and W ( s | A ) ⊆ I be the set of situations with the same syndrome s ; i.e., W ( s | A ) = { z ∈ I m | s ( z | A ) = s } ; W ( s | Z ; A ) = W ( s | A ) ∩ Z .

Definition 2. A WA A is said to: a) identify the situations in a set Z if the condition | W ( s | Z , A ) | = 1 is satisfied for all s ∈ S ( Z A ) ; b) identify the types of objects in a set Z if the condition | W + ( s | Z A ) | = 1 is satisfied for all s ∈ S ( Z A ) .

It is prooved in that for so-called suitable sets Z an algorithm of identification the types identifies also the situations in Z .

The perfect algorithms with parameters n = 11, m = 5, t = 2 are constructed in, which correspond to the parameters of the perfect ternary Golay code (Virtakallio-Golay code). A static algorithm (weighing code) with such parameters does not exist.

The Original Parallel Weighings Puzzle

Konstantin Knop invented this puzzle. We have N indistinguishable coins, one of which is fake (it is not known whether it is heavier or lighter than the genuine coins, which all weigh the same). There are two balance scales that can be used in parallel. Each weighing lasts one minute. What is the largest number of coins N for which it is possible to find the fake coin in five minutes?

In literature

Niobe, the protagonist of Piers Anthony's novel With a Tangled Skein, must solve the twelve-coin variation of this puzzle to find her son in Hell: Satan has disguised the son to look identical to eleven other demons, and he is heavier or lighter depending on whether he is cursed to lie or able to speak truthfully. The solution in the book follows the given example 1.c.

Beremiz, the main character from Júlio César de Mello e Souza's book The Man Who Counted, encounters an Indian merchant that challenges him with the standard balance puzzle with 8 identical shaped pearls (one pearl slightly lighter than the rest). Beremiz solves it by explicitly framing all the variables of the problem, using only two weighings.