Bakhshali manuscript

Discovery

The manuscript was discovered in 1881 by a peasant in the village of Bakhshali, which is near Peshawar, now in Pakistan. The first research on the manuscript was done by A. F. R. Hoernlé. After the death of Hoernle, it was examined by G. R. Kaye, who has edited the work and published it as a book in 1927.

The extant manuscript is incomplete, consisting of seventy leaves of birch bark. The intended order of the 70 leaves is indeterminate. It is currently housed in the Bodleian Library at the University of Oxford (MS. Sansk. d. 14) and is said to be too fragile to be examined by scholars.

Contents

The manuscript is a compendium of rules and illustrative example. Each example is stated as a problem, the solution is described, and it is verified that the problem has been solved. The sample problems are in verse and the commentary is in prose associated with calculations. The problems involve arithmetic, algebra and geometry, including mensuration. The topics covered include fractions, square roots, arithmetic and geometric progressions, solutions of simple equations, simultaneous linear equations, quadratic equations and indeterminate equations of the second degree.

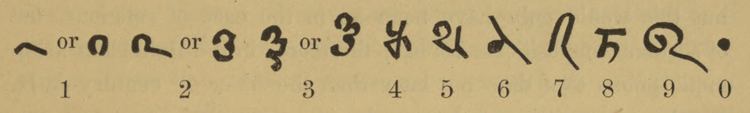
The manuscript is written in an earlier form of Śāradā script, which was mainly in use from the 8th to the 12th century, in the northwestern part of India, such as Kashmir and neighbouring regions. The language is the Gatha dialect (which is a combination of the ancient Indian languages of Sanskrit and Prakrit).

A colophon to one of the sections states that it was written by a brahmin identified as "the son of Chajaka", a "king of calculators," for the use of Vasiṣṭha's son Hasika. The brahmin might have been the author of the commentary as well as the scribe of the manuscript. Near the colophone appears a broken word rtikāvati, which has been interpreted as the place Mārtikāvata mentioned by Varāhamihira as being in northwestern India (along with Takṣaśilā, Gandhāra etc.), the supposed place where the manuscript might have been written.

Mathematics

The manuscript is a compilation of mathematical rules and examples (in verse), and prose commentaries on these verses. Typically, a rule is given, with an example or examples, where each example is followed by a "statement" (nyāsa / sthāpanā) of the example's numerical information in tabular form, then a computation that works out the example by following the rule step-by-step while quoting it, and finally a verification to confirm that the solution satisfies the problem. This is a style similar to that of Bhāskara I's commentary on the gaṇita (mathematics) chapter of the Āryabhaṭīya, including the emphasis on verification that became obsolete in later works.

The rules are algorithms and techniques for a variety of problems, such as systems of linear equations, quadratic equations, arithmetic progressions and arithmetico-geometric series, computing square roots approximately, dealing with negative numbers (profit and loss), measurement such as of the fineness of gold, etc.

Date

Its date is uncertain, and has generated considerable debate. Most scholars agree that the physical manuscript is a copy of a more ancient text, so that the dating of that ancient text is possible only based on the content. Hoernle thought that the manuscript was from the 9th century, but the original was from 3rd or 4th century. Kaye, on the other hand, thought the work was composed in the 12th century. Kaye's assessment is discounted in the current scholarship.

Indian scholars assign it an earlier date. Datta assigned it to the "early centuries of the Christian era." Channabasappa dates it to 200-400 CE, on the grounds that it uses mathematical terminology different from that of Aryabhata. Hayashi has stated that it was no later than the 7th century.

The dot symbol used as a zero the Bakhshali manuscript came to be called the shunya-bindu (literally, the dot of the empty place). References to the concept are found in Subandhu's Vasavadatta, which has been dated between 385 and 465 CE by the scholar Maan Singh.