 | ||
A single chemical reaction is said to have undergone autocatalysis, or be autocatalytic, if one of the reaction products is also a reactant and therefore a catalyst in the same or a coupled reaction. The reaction is called an autocatalytic reaction.
Contents
- Chemical reactions
- Chemical equilibrium
- Far from equilibrium
- Autocatalytic reactions
- Background
- Temporal order
- Idealized example Lotka Volterra equation
- Another idealized example Brusselator
- Spatial order
- Real examples
- Optics example
- Biological example
- Phase transitions
- Asymmetric autocatalysis
- Role in origin of life
- Examples of autocatalytic reactions
- References
The rate equations for autocatalytic reactions are fundamentally nonlinear. This nonlinearity can lead to the spontaneous generation of order. A dramatic example of this order is that which is found in living systems. The spontaneous order creation corresponds to a decrease in the entropy of the system, which must be compensated by a larger increase in the entropy of the surroundings in order to satisfy the Second Law of Thermodynamics.
A set of chemical reactions can be said to be "collectively autocatalytic" if a number of those reactions produce, as reaction products, catalysts for enough of the other reactions that the entire set of chemical reactions is self-sustaining given an input of energy and food molecules (see autocatalytic set).
Chemical reactions
A chemical reaction of two reactants and two products can be written as
where the Greek letters are stoichiometric coefficients and the capital Latin letters represent chemical species. The chemical reaction proceeds in both the forward and reverse direction. This equation is easily generalized to any number of reactants, products, and reactions.
Chemical equilibrium
In chemical equilibrium the forward and reverse reaction rates are such that each chemical species is being created at the same rate it is being destroyed. In other words, the rate of the forward reaction is equal to the rate of the reverse reaction.
Here, the brackets indicate the concentration of the chemical species, in moles per liter, and k+ and k− are rate constants.
Far from equilibrium
Far from equilibrium, the forward and reverse reaction rates no longer balance and the concentration of reactants and products is no longer constant. For every forward reaction
This system of equations has a single stable fixed point when the forward rates and the reverse rates are equal. This means that the system evolves to the equilibrium state, and this is the only state to which it evolves.
Autocatalytic reactions
Autocatalytic reactions are those in which at least one of the products is a reactant. Perhaps the simplest autocatalytic reaction can be written
with the rate equations (for an elementary reaction)
This reaction is one in which a molecule of species A interacts with a molecule of species B. The A molecule is converted into a B molecule. The final product consists of the original B molecule plus the B molecule created in the reaction.
The key feature of these rate equations is that they are nonlinear; the second term on the right varies as the square of the concentration of B. This feature can lead to multiple fixed points of the system, much like a quadratic equation can have multiple roots. Multiple fixed points allow for multiple states of the system. A system existing in multiple macroscopic states is more orderly (has lower entropy) than a system in a single state.
The concentrations of A and B vary in time according to
and
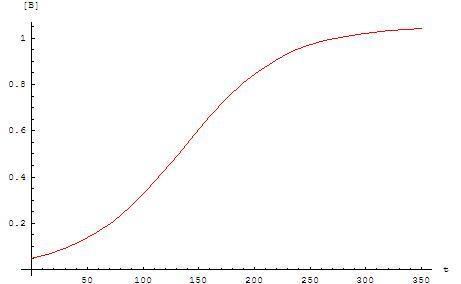
The graph for these equations is a sigmoid curve, which is typical for autocatalytic reactions: these chemical reactions proceed slowly at the start (the induction period) because there is little catalyst present, the rate of reaction increases progressively as the reaction proceeds as the amount of catalyst increases and then it again slows down as the reactant concentration decreases. If the concentration of a reactant or product in an experiment follows a sigmoid curve, the reaction may be autocatalytic.
These kinetic equations apply for example to the acid-catalyzed hydrolysis of some esters to carboxylic acids and alcohols. There must be at least some acid present initially to start the catalyzed mechanism; if not the reaction must start by an alternate uncatalyzed path which is usually slower. The above equations for the catalyzed mechanism would imply that the concentration of acid product remains zero forever.
Background
The Second Law of Thermodynamics states that the disorder (entropy) of a physical or chemical system and its surroundings (a closed system) must increase with time. Systems left to themselves become increasingly random, and orderly energy of a system like uniform motion degrades eventually to the random motion of particles in a heat bath.
There are, however, many instances in which physical systems spontaneously become emergent or orderly. For example, despite the destruction they cause, hurricanes have a very orderly vortex motion when compared to the random motion of the air molecules in a closed room. Even more spectacular is the order created by chemical systems; the most dramatic being the order associated with life.
This is consistent with the Second Law, which requires that the total disorder of a system and its surroundings must increase with time. Order can be created in a system by an even greater decrease in order of the systems surroundings. In the hurricane example, hurricanes are formed from unequal heating within the atmosphere. The Earth's atmosphere is then far from thermal equilibrium. The order of the Earth's atmosphere increases, but at the expense of the order of the sun. The sun is becoming more disorderly as it ages and throws off light and material to the rest of the universe. The total disorder of the sun and the earth increases despite the fact that orderly hurricanes are generated on earth.
A similar example exists for living chemical systems. The sun provides energy to green plants. The green plants are food for other living chemical systems. The energy absorbed by plants and converted into chemical energy generates a system on earth that is orderly and far from chemical equilibrium. Here, the difference from chemical equilibrium is determined by an excess of reactants over the equilibrium amount. Once again, order on earth is generated at the expense of entropy increase of the sun. The total entropy of the earth and the rest of the universe increases, consistent with the Second Law.
Some autocatalytic reactions also generate order in a system at the expense of its surroundings. For example, (clock reactions) have intermediates whose concentrations oscillate in time, corresponding to temporal order. Other reactions generate spatial separation of chemical species corresponding to spatial order. More complex reactions are involved in metabolic pathways and metabolic networks in biological systems.
The transition to order as the distance from equilibrium increases is not usually continuous. Order typically appears abruptly. The threshold between the disorder of chemical equilibrium and order is known as a phase transition. The conditions for a phase transition can be determined with the mathematical machinery of non-equilibrium thermodynamics.
Temporal order
A chemical reaction cannot oscillate about a position of final equilibrium because the second law of thermodynamics requires that a thermodynamic system approach equilibrium and not recede from it. For a closed system at constant temperature and pressure, the Gibbs free energy must decrease continuously and not oscillate. However it is possible that the concentrations of some reaction intermediates oscillate, and also that the rate of formation of products oscillates.
Idealized example: Lotka-Volterra equation
Consider a coupled set of two autocatalytic reactions in which the concentration of one of the reactants A is much larger than its equilibrium value. In this case the forward reaction rate is so much larger than the reverse rates that we can neglect the reverse rates.
with the rate equations
Here, we have neglected the depletion of the reactant A, since its concentration is so large. The rate constants for the three reactions are
This system of rate equations is known as the Lotka-Volterra equation and is most closely associated with population dynamics in predator-prey relationships. This system of equations can yield oscillating concentrations of the reaction intermediates X and Y. The amplitude of the oscillations depends on the concentration of A (which decreases without oscillation). Such oscillations are a form of emergent temporal order that is not present in equilibrium.
Another idealized example: Brusselator
Another example of a system that demonstrates temporal order is the Brusselator (see Prigogine reference). It is characterized by the reactions
with the rate equations
where, for convenience, the rate constants have been set to 1.
The Brusselator has a fixed point at
The fixed point becomes unstable when
leading to an oscillation of the system. Unlike the Lotka-Volterra equation, the oscillations of the Brusselator do not depend on the amount of reactant present initially. Instead, after sufficient time, the oscillations approach a limit cycle.
Spatial order
An idealized example of spatial spontaneous symmetry breaking is the case in which we have two boxes of material separated by a permeable membrane so that material can diffuse between the two boxes. It is assumed that identical Brusselators are in each box with nearly identical initial conditions. (see Prigogine reference)
Here, the numerical subscripts indicate which box the material is in. There are additional terms proportional to the diffusion coefficient D that account for the exchange of material between boxes.
If the system is initiated with the same conditions in each box, then a small fluctuation will lead to separation of materials between the two boxes. One box will have a predominance of X, and the other will have a predominance of Y.
Real examples
Real examples of clock reactions are the Belousov-Zhabotinsky reaction (BZ reaction), the Briggs-Rauscher reaction, the Bray-Liebhafsky reaction and the iodine clock reaction. These are oscillatory reactions, and the concentration of products and reactants can be approximated in terms of damped oscillations.
The best-known reaction, the BZ reaction, can be created with a mixture of potassium bromate
Optics example
Another autocatalytic system is one driven by light coupled to photo-polymerization reactions. In a process termed optical autocatalysis, positive feedback is created between light intensity and photo-polymerization rate, via polymerization-induced increases in the refractive index. Light's preference to occupy regions of higher refractive index results in leakage of light into regions of higher molecular weight, thereby amplifying the photo-chemical reaction. The positive feedback may be expressed as:
Noting that photo-polymerization rate is proportional to intensity and that refractive index is proportional to molecular weight, the positive feedback between intensity and photo-polymerization establishes the auto-catalytic behavior. Optical auto-catalysis has been shown to result on spontaneous pattern formation in photopolymers. Hosein and co-workers discovered that optical autocatalysis can also occur in photoreactive polymer blends, and that the process can induce binary phase morphologies with the same pattern as the light profile. The light undergoes optical modulation instability, spontaneous dividing into a multitude of optical filaments, and the polymer system thereby forms filaments within the blend structure. The result is a new system that couples optical autocatalytic behavior to spinodal decompositon.
Biological example
It is known that an important metabolic cycle, glycolysis, displays temporal order. Glycolysis consists of the degradation of one molecule of glucose and the overall production of two molecules of ATP. The process is therefore of great importance to the energetics of living cells. The global glycolysis reaction involves glucose, ADP, NAD, pyruvate, ATP, and NADH.
The details of the process are quite involved, however, a section of the process is autocatalyzed by phosphofructokinase (PFK). This portion of the process is responsible for oscillations in the pathway that lead to the process oscillating between an active and an inactive form. Thus, the autocatalytic reaction can modulate the process.
Phase transitions
The initial amounts of reactants determine the distance from chemical equilibrium of the system. The greater the initial concentrations the further the system is from equilibrium. As the initial concentration increases, an abrupt change in order occurs. This abrupt change is known as phase transition. At the phase transition, fluctuations in macroscopic quantities, such as chemical concentrations, increase as the system oscillates between the more ordered state (lower entropy, such as ice) and the more disordered state (higher entropy, such as liquid water). Also, at the phase transition, macroscopic equations, such as the rate equations, fail. Rate equations can be derived from microscopic considerations. The derivations typically rely on a mean field theory approximation to microscopic dynamical equations. Mean field theory breaks down in the presence of large fluctuations (see Mean field theory article for a discussion). Therefore, since large fluctuations occur in the neighborhood of a phase transition, macroscopic equations, such as rate equations, fail. As the initial concentration increases further, the system settles into an ordered state in which fluctuations are again small. (see Prigogine reference)
Asymmetric autocatalysis
Asymmetric autocatalysis occurs when the reaction product is chiral and thus acts as a chiral catalyst for its own production. Reactions of this type, such as the Soai reaction, have the property that they can amplify a very small enantiomeric excess into a large one. This has been proposed as an important step in the origin of biological homochirality.
Role in origin of life
In 1995 Stuart Kauffman proposed that life initially arose as autocatalytic chemical networks.
British ethologist Richard Dawkins wrote about autocatalysis as a potential explanation for abiogenesis in his 2004 book The Ancestor's Tale. He cites experiments performed by Julius Rebek and his colleagues at the Scripps Research Institute in California in which they combined amino adenosine and pentafluorophenyl ester with the autocatalyst amino adenosine triacid ester (AATE). One system from the experiment contained variants of AATE which catalysed the synthesis of themselves. This experiment demonstrated the possibility that autocatalysts could exhibit competition within a population of entities with heredity, which could be interpreted as a rudimentary form of natural selection, and that certain environmental changes (such as irradiation) could alter the chemical structure of some of these self-replicating molecules (an analogue for mutation) in such ways that could either boost or interfere with its ability to react, thus boosting or interfering with its ability to replicate and spread in the population.
Autocatalysis plays a major role in the processes of life. Two researchers who have emphasised its role in the origins of life are Robert Ulanowicz and Stuart Kauffman.
Autocatalysis occurs in the initial transcripts of rRNA. The introns are capable of excising themselves by the process of two nucleophilic transesterification reactions. The RNA able to do this is sometimes referred to as a ribozyme. Additionally, the citric acid cycle is an autocatalytic cycle run in reverse.
Ultimately, biological metabolism itself can be seen as a vast autocatalytic set, in that all of the molecular constituents of a biological cell are produced by reactions involving this same set of molecules.
