 | ||
In mathematics, particularly topology, one describes a manifold using an atlas. An atlas consists of individual charts that, roughly speaking, describe individual regions of the manifold. If the manifold is the surface of the Earth, then an atlas has its more common meaning. In general, the notion of atlas underlies the formal definition of a manifold and related structures such as vector bundles and other fibre bundles.
Contents
Charts
The definition of an atlas depends on the notion of a chart. A chart for a topological space M (also called a coordinate chart, coordinate patch, coordinate map, or local frame) is a homeomorphism
Formal definition of atlas
An atlas for a topological space M is a collection
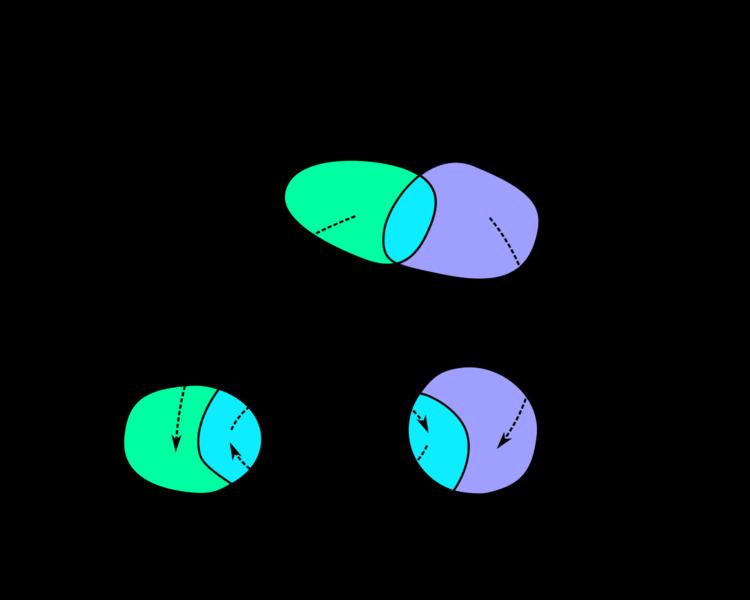
Transition maps
A transition map provides a way of comparing two charts of an atlas. To make this comparison, we consider the composition of one chart with the inverse of the other. This composition is not well-defined unless we restrict both charts to the intersection of their domains of definition. (For example, if we have a chart of Europe and a chart of Russia, then we can compare these two charts on their overlap, namely the European part of Russia.)
To be more precise, suppose that
Note that since
More structure
One often desires more structure on a manifold than simply the topological structure. For example, if one would like an unambiguous notion of differentiation of functions on a manifold, then it is necessary to construct an atlas whose transition functions are differentiable. Such a manifold is called differentiable. Given a differentiable manifold, one can unambiguously define the notion of tangent vectors and then directional derivatives.
If each transition function is a smooth map, then the atlas is called a smooth atlas, and the manifold itself is called smooth. Alternatively, one could require that the transition maps have only k continuous derivatives in which case the atlas is said to be
Very generally, if each transition function belongs to a pseudo-group
