Asymmetric Numeral Systems

Entropy coding

Imagine you want to encode a length 1000 sequence of zeros and ones, what directly takes 1000 bits to store. However, if it is somehow known that it only contains 1 zero and 999 ones, it would be sufficient to encode the zero position, what requires only ⌈ log 2 ⁡ ( 1000 ) ⌉ = 10 bits here instead of the original 1000 bits.

Generally, such length n sequences containing p n zeros and ( 1 − p ) n ones, for some probability p ∈ ( 0 , 1 ) , are called combinations. Using Stirling's approximation we get their asymptotic number being

( n p n ) ≈ 2 n h ( p ) for large n and h ( p ) = − p log 2 ⁡ ( p ) − ( 1 − p ) log 2 ⁡ ( 1 − p ) called Shannon entropy.

Hence, to choose one of such sequences we need approximately n h ( p ) bits. It is still n bits if p = 1 / 2 , however, it can also be much smaller. For example we need only ≈ n / 2 bits for p = 0.11 .

Entropy coder allows to encode a sequence of symbols using approximately Shannon entropy bits/symbol. For example ANS could be directly used to enumerate combinations: assign a different natural number to every sequence of symbols having fixed proportions in nearly optimal way.

In contrast to encoding combinations, this probability distribution usually varies in data compressors. For this purpose, Shannon entropy can be seen as weighted average: that symbol of probability p contains log 2 ⁡ ( 1 / p ) bits of information. ANS encodes information into a single natural number x , interpreted as containing log 2 ⁡ ( x ) bits of information. Adding to it information from a symbol of probability p , increases this informational content to log 2 ⁡ ( x ) + log 2 ⁡ ( 1 / p ) = log 2 ⁡ ( x / p ) . Hence, the new number containing both information should be x ′ ≈ x / p .

Basic concepts of ANS

Imagine there is some information stored in a natural number x , for example as bit sequence of its binary expansion. To add information from a binary variable s , we can use coding function x ′ = C ( x , s ) = 2 x + s , which shifts all bits one position up, and place the new bit in the least significant position. Now decoding function D ( x ′ ) = ( ⌊ x ′ / 2 ⌋ , m o d ( x ′ , 2 ) ) allows to retrieve the previous x and this added bit: D ( C ( x , s ) ) = ( x , s ) ,   C ( D ( x ′ ) ) = x ′ . We can start with x = 1 initial state, then use the C function on the successive bits of a finite bit sequence to obtain a final x number storing this entire sequence. Then using D function multiple times until x = 1 allows to retrieve the bit sequence in reversed order.

The above procedure is optimal for uniform (symmetric) probability distribution of symbols Pr ( 0 ) = Pr ( 1 ) = 1 / 2 . ANS generalize it to make it optimal for any chosen (asymmetric) probability distribution of symbols: Pr ( s ) = p s . While s in the above example was choosing between even and odd C ( x , s ) , in ANS this even/odd division of natural numbers is replaced with division into subsets having densities corresponding to the assumed probability distribution { p s } s : up to position x , there is approximately x p s occurrences of symbol s .

The coding function C ( x , s ) returns the x -th appearance from such subset corresponding to symbol s . The density assumption is equivalent to condition x ′ = C ( x , s ) ≈ x / p s . Assuming that a natural number x contains log 2 ⁡ ( x ) bits information, log 2 ⁡ ( C ( x , s ) ) ≈ log 2 ⁡ ( x ) + log 2 ⁡ ( 1 / p s ) . Hence the symbol of probability p s is encoded as containing ≈ log 2 ⁡ ( 1 / p s ) bits of information as it is required from entropy coders.

Uniform binary variant (uABS)

Let us start with binary alphabet and probability distribution Pr ( 1 ) = p , Pr ( 0 ) = 1 − p . Up to position x we want approximately p ⋅ x analogues of odd numbers (for s = 1 ). We can choose this number of appearances as ⌈ x ⋅ p ⌉ , getting s = ⌈ ( x + 1 ) ⋅ p ⌉ − ⌈ x ⋅ p ⌉ . This is called uABS variant and leads to the following decoding and encoding functions:

Decoding:

Encoding:

For p = 1 / 2 it becomes standard binary system (with switched 0 and 1), for a different p it becomes optimal for this given probability distribution. For example, for p = 0.3 these formulas lead to table for small values of x :

Symbol s = 1 corresponds to subset of natural numbers of density p = 0.3 , which in this case are positions { 0 , 3 , 6 , 10 , 13 , 16 , 20 , 23 , 26 , … } . As 1 / 4 < 0.3 < 1 / 3 , these positions increase by 3 or 4. Because p = 3 / 10 here, the pattern of symbols repeats every 10 positions.

The C ( x , s ) can be found by taking row corresponding to a given symbol s , and take given x in this row. Then top row provides C ( x , s ) . For example, C ( 7 , 0 ) = 11 from the middle to top row.

Imagine we would like to encode '0100' sequence starting from x = 1 . First s = 0 takes us to x = 2 , then s = 1 to x = 6 , then s = 0 to x = 9 , then s = 0 to x = 14 . By using decoding function D ( x ′ ) on this final x , we can retrieve the symbol sequence. Using the table for this purpose, x in first row determines column, then nonempty row and the written value determine correspondingly s and x .

Range variants (rANS) and streaming

Range variant also uses arithmetic formulas, but allows to operate on large alphabet. Intuitively, it divides the set of natural numbers into size 2 n ranges, and split each of them in identical way into subranges of proportions given by the assumed probability distribution.

We start with quanization of probability distribution to 2 n denominator, where n is chosen (usually 8-12 bits): p s ≈ f [ s ] / 2 n for some natural f [ s ] numbers (sizes of subranges).

Denote mask = 2 n − 1 , cumulative distribution function: CDF ⁡ [ s ] = ∑ i < s f [ i ] = f [ 0 ] + … + f [ s − 1 ] .

For y ∈ [ 0 , 2 n − 1 ] denote function (usually tabled)

symbol(y) = s such that CDF[s] <= y < CDF[s+1] .

Now coding function is:

C(x,s) = (floor(x / f[s]) << n) + (x % f[s]) + CDF[s]

Decoding: s = symbol(x & mask)

D(x) = (f[s] * (x >> n) + (x & mask ) - CDF[s], s)

This way we can encode a sequence of symbols into a large natural number x . To avoid using large number arithmetic, in practice stream variants are used: which enforce x ∈ [ L , b ⋅ L − 1 ] by renormalization: sending the least significant bits of x to or from the bitstream (usually L and b are powers of 2).

In rANS variant x is for example 32 bit. For 16 bit renormalization, x ∈ [ 2 16 , 2 32 − 1 ] , decoder refills the least significant bits from the bitstream when needed:

if(x < (1 << 16)) x = (x << 16) + read16bits()

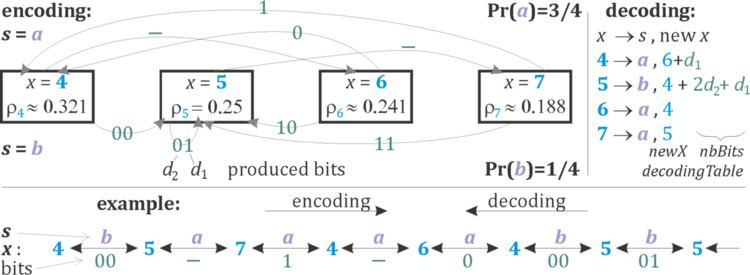
Tabled variant (tANS)

tANS variant puts the entire behavior (including renormalization) for x ∈ [ L , 2 L − 1 ] into a table, getting finite state machine avoiding the need of multiplication.

Finally step of decoding loop can be written as:

Step of encoding loop:

A specific tANS coding is determined by assigning a symbol to every [ L , 2 L − 1 ] position, their number of appearances should be proportional to the assumed probabilities. For example one could choose "abdacdac" assignment for Pr(a)=3/8, Pr(b)=1/8, Pr(c)=2/8, Pr(d)=2/8 probability distribution. If symbols are assigned in ranges of lengths being powers of 2, we would get Huffman coding. For example a->0, b->100, c->101, d->11 prefix code would be obtained for tANS with "aaaabcdd" symbol assignment.

Remarks

As for Huffman coding, modifying the probability distribution of tANS is costly, hence they are used in static situations, usually with some Lempel–Ziv scheme (ZSTD, LZFSE). In this case, the file is divided into blocks and static probability distribution for each block is stored in its header.

In contrast, rANS is usually used as faster replacement for range coding. It requires multiplication, but is more memory efficient and is appropriate for dynamically adapting probability distributions.

Encoding and decoding of ANS are performed in opposite directions. This inconvenience is usually resolved by encoding in backward direction, thanks of it decoding can made forward. For context-dependence, like Markov model, the encoder needs to use context from the perspective of decoder. For adaptivity, the encoder should first go forward to find probabilities which will be used by decoder and store them in a buffer, then encode in backward direction using the found probabilities.

The final state of encoding is required to start decoding, hence it needs to be stored in the compressed file. This cost can be compensated by storing some information in the initial state of encoder.