Andrica's conjecture (named after Dorin Andrica) is a conjecture regarding the gaps between prime numbers.
The conjecture states that the inequality
p n + 1 − p n < 1 holds for all n , where p n is the nth prime number. If g n = p n + 1 − p n denotes the nth prime gap, then Andrica's conjecture can also be rewritten as
g n < 2 p n + 1. Imran Ghory has used data on the largest prime gaps to confirm the conjecture for n up to 1.3002 × 1016. Using a table of maximal gaps and the above gap inequality, the confirmation value can be extended exhaustively to 4 × 1018.
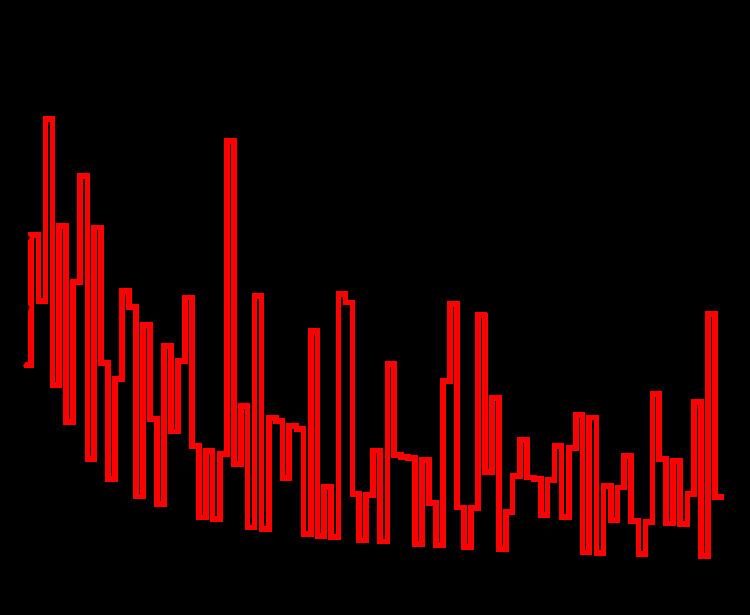
The discrete function A n = p n + 1 − p n is plotted in the figures opposite. The high-water marks for A n occur for n = 1, 2, and 4, with A4 ≈ 0.670873..., with no larger value among the first 105 primes. Since the Andrica function decreases asymptotically as n increases, a prime gap of ever increasing size is needed to make the difference large as n becomes large. It therefore seems highly likely the conjecture is true, although this has not yet been proven.
As a generalization of Andrica's conjecture, the following equation has been considered:
p n + 1 x − p n x = 1 , where p n is the nth prime and x can be any positive number.
The largest possible solution x is easily seen to occur for n = 1 , when xmax = 1. The smallest solution x is conjectured to be xmin ≈ 0.567148... (sequence A038458 in the OEIS) which occurs for n = 30.
This conjecture has also been stated as an inequality, the generalized Andrica conjecture:
p n + 1 x − p n x < 1 for
x < x min .