Absolute magnitude

Stars and galaxies (M)

In stellar and galactic astronomy, the standard distance is 10 parsecs (about 32.616 light years, 308.57 petameters or 308.57 trillion kilometres). A star at 10 parsecs has a parallax of 0.1″ (100 milliarcseconds). Galaxies (and other extended objects) are much larger than 10 parsecs, their light is radiated over an extended patch of sky, and their overall brightness cannot be directly observed from relatively short distances, but the same convention is used. A galaxy's magnitude is defined by measuring all the light radiated over the entire object, treating that integrated brightness as the brightness of a single point-like or star-like source, and computing the magnitude of that point-like source as it would appear if observed at the standard 10 parsecs distance. Consequently, the absolute magnitude of any object equals the apparent magnitude it would have if it were 10 parsecs away.

The measurement of absolute magnitude is made with an instrument called a bolometer. When using an absolute magnitude, one must specify the type of electromagnetic radiation being measured. When referring to total energy output, the proper term is bolometric magnitude. The bolometric magnitude usually is computed from the visual magnitude plus a bolometric correction, M_bol = M_V + BC. This correction is needed because very hot stars radiate mostly ultraviolet radiation, whereas very cool stars radiate mostly infrared radiation (see Planck's law).

Many stars visible to the naked eye have such a low absolute magnitude that they would appear bright enough to cast shadows if they were at 10 parsecs from the Earth: Rigel (−7.0), Deneb (−7.2), Naos (−6.0), and Betelgeuse (−5.6). For comparison, Sirius has an absolute magnitude of 1.4, which is brighter than the Sun, whose absolute visual magnitude is 4.83 (it actually serves as a reference point). The Sun's absolute bolometric magnitude is set arbitrarily, usually at 4.75. Absolute magnitudes of stars generally range from −10 to +17. The absolute magnitudes of galaxies can be much lower (brighter). For example, the giant elliptical galaxy M87 has an absolute magnitude of −22 (i.e. as bright as about 60,000 stars of magnitude −10).

Apparent magnitude

The Greek astronomer Hipparchus established a numerical scale to describe the brightness of each star appeared in the sky. The brightest stars in the sky were assigned an apparent magnitude m = 1, and the dimmest stars visible to the naked eye are assigned m = 6. The difference between them corresponds to a factor of 100 in brightness. For objects within the Milky Way, the absolute magnitude M and apparent magnitude m from any distance d (in parsecs) is related by:

100 m − M 5 = F 10 F = ( d 10 p c ) 2 ,

where F is the radiant flux measured at distance d (in parsecs), F₁₀ the radiant flux measured at distance d = 10 pc. The relation can be written in terms of logarithm:

M = m − 5 ( log 10 ⁡ d − 1 ) ,

where the insignificance of extinction by gas and dust is assumed.

For objects at very large distances (outside the Milky Way) the luminosity distance d_L must be used instead of d (in parsecs), because the Euclidean approximation is invalid for distant objects and general relativity must be taken into account. Moreover, the cosmological redshift complicates the relation between absolute and apparent magnitude, because the radiation observed was shifted into the red range of the spectrum. To compare the magnitudes of very distant objects with those of local objects, a K correction might have to be applied to the magnitudes of the distant objects.

The absolute magnitude M can also be approximated using apparent magnitude m and stellar parallax p:

M = m + 5 ( log 10 ⁡ p + 1 ) ,

or using apparent magnitude m and distance modulus μ:

M = m − μ .

Examples

Rigel has a visual magnitude m_V of 0.12 and distance about 860 light-years

M V = 0.12 − 5 ( log 10 ⁡ 860 3.2616 − 1 ) = − 7.0.

Vega has a parallax p of 0.129″, and an apparent magnitude m_V of 0.03

M V = 0.03 + 5 ( log 10 ⁡ 0.129 + 1 ) = + 0.6.

Alpha Centauri A has a parallax p of 0.742″ and an apparent magnitude m_V of −0.01

M V = − 0.01 + 5 ( log 10 ⁡ 0.742 + 1 ) = + 4.3.

The Black Eye Galaxy has a visual magnitude m_V of 9.36 and a distance modulus μ of 31.06

M V = 9.36 − 31.06 = − 21.7.

Bolometric magnitude

The bolometric magnitude M_bol, takes into account electromagnetic radiation at all wavelengths. It includes those unobserved due to instrumental pass-band, the Earth's atmospheric absorption, and extinction by interstellar dust. It is defined based on the luminosity of the stars. In the case of stars with few observations, it must be computed assuming an effective temperature.

Classically, the difference in bolometric magnitude is related to the luminosity ratio according to:

M b o l , ⋆ − M b o l , ⊙ = − 2.5 log 10 ⁡ ( L ⋆ L ⊙ )

which makes by inversion:

L ⋆ L ⊙ = 10 0.4 ( M b o l , ⊙ − M b o l , ⋆ )

where

L_⊙ is the Sun's luminosity (bolometric luminosity) L_★ is the star's luminosity (bolometric luminosity) M_bol,⊙ is the bolometric magnitude of the Sun M_bol,★ is the bolometric magnitude of the star.

In August 2015, the International Astronomical Union passed Resolution B2 defining the zero points of the absolute and apparent bolometric magnitude scales in SI units for power (watts) and irradiance (W/m²), respectively. Although bolometric magnitudes had been used by astronomers for many decades, there had been systematic differences in the absolute magnitude-luminosity scales presented in various astronomical references, and no international standardization. This led to systematic differences in bolometric corrections scales, which when combined with incorrect assumed absolute bolometric magnitudes for the Sun could lead to systematic errors in estimated stellar luminosities (and stellar properties calculated which rely on stellar luminosity, such as radii, ages, and so on).

Resolution B2 defines an absolute bolometric magnitude scale where M_bol = 0 corresponds to luminosity L₀ = 7028301280000000000♠3.0128×10²⁸ W, with the zero point luminosity L₀ set such that the Sun (with nominal luminosity 7026382800000000000♠3.828×10²⁶ W) corresponds to absolute bolometric magnitude M_bol,⊙ = 4.74. Placing a radiation source (e.g. star) at the standard distance of 10 parsecs, it follows that the zero point of the apparent bolometric magnitude scale m_bol = 0 corresponds to irradiance f₀ = 6992251802100199999♠2.518021002×10⁻⁸ W/m². Using the IAU 2015 scale, the nominal total solar irradiance ("solar constant") measured at 1 astronomical unit (7003136100000000000♠1361 W/m²) corresponds to an apparent bolometric magnitude of the Sun of m_bol,⊙ = −26.832.

Following Resolution B2, the relation between a star's absolute bolometric magnitude and its luminosity is no longer directly tied to the Sun's (variable) luminosity:

M b o l = − 2.5 log 10 ⁡ L ⋆ L 0 = − 2.5 log 10 ⁡ L ⋆ + 71.197425...

where

L_★ is the star's luminosity (bolometric luminosity) in watts L₀ is the zero point luminosity 7028301280000000000♠3.0128×10²⁸ W M_bol is the bolometric magnitude of the star

The new IAU absolute magnitude scale permanently disconnects the scale from the variable Sun. However, on this SI power scale, the nominal solar luminosity corresponds closely to M_bol = 4.74, a value that was commonly adopted by astronomers before the 2015 IAU resolution.

The luminosity of the star in watts can be calculated as a function of its absolute bolometric magnitude M_bol as:

L ⋆ = L 0 10 − 0.4 M B o l

using the variables as defined previously.

Solar System bodies (H)

For planets and asteroids a definition of absolute magnitude that is more meaningful for nonstellar objects is used.

In this case, the absolute magnitude (H) is defined as the apparent magnitude that the object would have if it were one astronomical unit (AU) from both the Sun and the observer. Because the object is illuminated by the Sun, absolute magnitude is a function of phase angle and this relationship is referred to as the phase curve.

To convert a stellar or galactic absolute magnitude into a planetary one, subtract 31.57. A comet's nuclear magnitude (M₂) is a different scale and can not be used for a size comparison with an asteroid's (H) magnitude.

Apparent magnitude

The absolute magnitude can be used to help calculate the apparent magnitude of a body under different conditions.

m = H + 2.5 log 10 ⁡ ( d B S 2 d B O 2 p ( χ ) d 0 4 )

where d₀ is 1 AU, χ is the phase angle, the angle between the Sun–body and body–observer lines. By the law of cosines, we have:

cos ⁡ χ = d B O 2 + d B S 2 − d O S 2 2 d B O d B S .

p(χ) is the phase integral (integration of reflected light; a number in the 0 to 1 range).

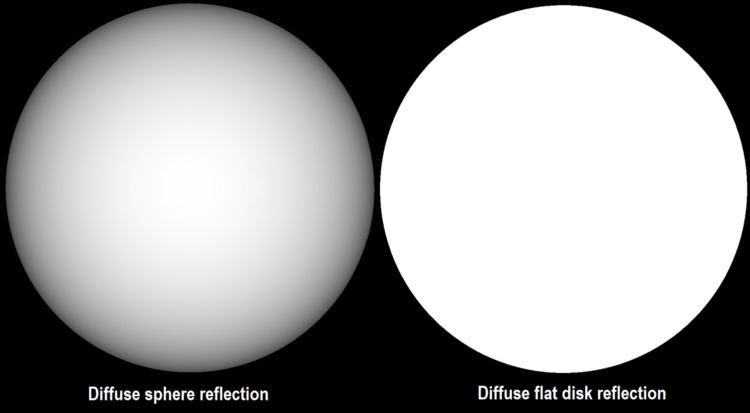
Example: Ideal diffuse reflecting sphere. A reasonable first approximation for planetary bodies

p ( χ ) = 2 3 ( ( 1 − χ π ) cos ⁡ χ + 1 π sin ⁡ χ ) .

A full-phase diffuse sphere reflects 2/3 as much light as a diffuse disc of the same diameter.

Distances:

d_BO is the distance between the observer and the body

d_BS is the distance between the Sun and the body

d_OS is the distance between the observer and the Sun

Note: because Solar System bodies are never perfect diffuse reflectors, astronomers use empirically derived relationships to predict apparent magnitudes when accuracy is required.

Example

Moon:

H_Moon = +0.25

d_OS = d_BS = 1 AU

d_BO = 7008384500000000000♠3.845×10⁸ m = 7008384466527698999♠0.00257 AU

How bright is the Moon from Earth?

Full moon: χ = 0, p(χ) ≈ 2/3 m M o o n = 0.25 + 2.5 log 10 ⁡ ( 3 2 ⋅ 0.00257 2 ) = − 12.26 Actual value: −12.7. A full Moon reflects 30% more light than a perfect diffuse reflector predicts.

Quarter moon: χ = 90° = π/2, p(χ) ≈ 2/3π (if diffuse reflector) m M o o n = 0.25 + 2.5 log 10 ⁡ ( 3 π 2 ⋅ 0.00257 2 ) = − 11.02 Actual value: approximately −11. The diffuse reflector formula does well for smaller phases.

Meteors

For a meteor, the standard distance for measurement of magnitudes is at an altitude of 100 km (62 mi) at the observer's zenith.