 | ||
ACC0, sometimes called ACC, is a class of computational models and problems defined in circuit complexity, a field of theoretical computer science. The class is defined by augmenting the class AC0 of constant-depth "alternating circuits" with the ability to count; the acronym ACC stands for "AC with counters". Specifically, a problem belongs to ACC0 if it can be solved by polynomial-size, constant-depth circuits of unbounded fan-in gates, including gates that count modulo a fixed integer. ACC0 corresponds to computation in any solvable monoid. The class is very well studied in theoretical computer science because of the algebraic connections and because it is one of the largest concrete computational models for which computational impossibility results, so-called circuit lower bounds, can be proved.
Contents
Definitions
Informally, ACC0 models the class of computations realised by Boolean circuits of constant depth and polynomial size, where the circuit gates includes "modular counting gates" that compute the number of true inputs modulo some fixed constant.
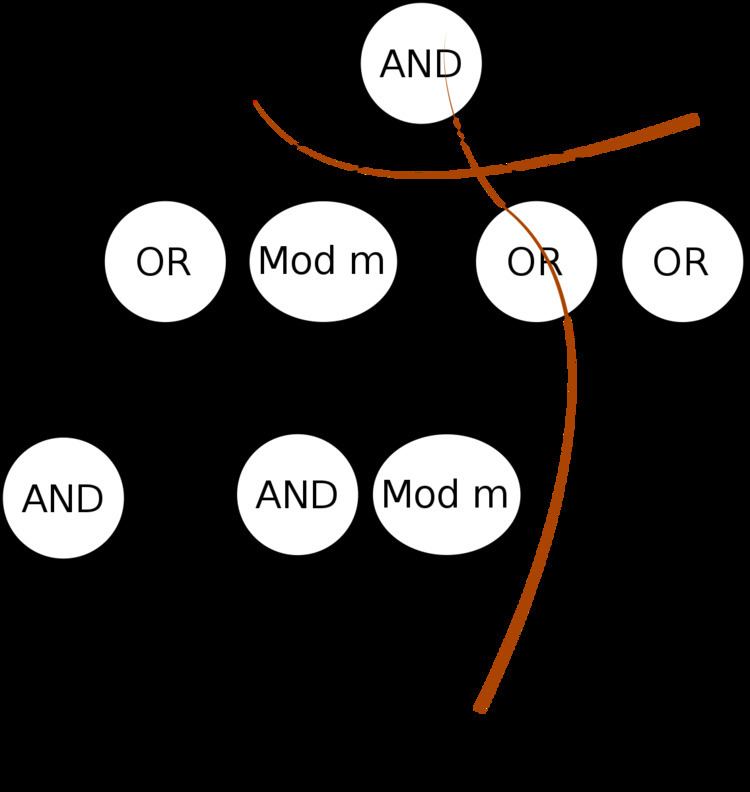
More formally, a language belongs to AC0[m] if it can be computed by a family of circuits C1, C2, ..., where Cn takes n inputs, the depth of every circuit is constant, the size of Cn is a polynomial function of n, and the circuit uses the following gates: AND gates and OR gates of unbounded fan-in, computing the conjunction and disjunction of their inputs; NOT gates computing the negation of their single input; and unbounded fan-in MOD-m gates, which compute 1 if the number of input 1s is a multiple of m. A language belongs to ACC0 if it belongs to AC0[m] for some m.
In some texts, ACCi refers to a hierarchy of circuit classes with ACC0 at its lowest level, where the circuits in ACCi have depth O(login) and polynomial size.
The class ACC0 can also be defined in terms of computations of nonuniform deterministic finite automata (NUDFA) over monoids. In this framework, the input is interpreted as elements from a fixed monoid, and the input is accepted if the product of the input elements belongs to a given list of monoid elements. The class ACC0 is the family of languages accepted by a NUDFA over some monoid that does not contain an unsolvable group as a subsemigroup.
Computational power
The class ACC0 includes AC0. This inclusion is strict, because a single MOD-2 gate computes the parity function, which is known to be impossible to compute in AC0. More generally, the function MODm can not be computed in AC0[p] for prime p unless m is a power of p.
The class ACC0 is included in TC0. It is conjectured that ACC0 is unable to compute the majority function of its inputs (i.e. the inclusion in TC0 is strict), but this remains unresolved as of July 2014.
Every problem in ACC0 can be solved by circuits of depth 2, with AND gates of polylogarithmic fan-in at the inputs, connected to a single gate computing a symmetric function. These circuits are called SYM+-circuits. The proof follows ideas of the proof of Toda's theorem.
Williams (2011) proves that ACC0 does not contain NEXPTIME. The proof uses many results in complexity theory, including the time hierarchy theorem, IP = PSPACE, derandomization, and the representation of ACC0 via SYM+ circuits.
It is known that computing the permanent is impossible for logtime-uniform ACC0 circuits, which implies that the complexity class PP is not contained in logtime-uniform ACC0.
