Samiksha Jaiswal (Editor)

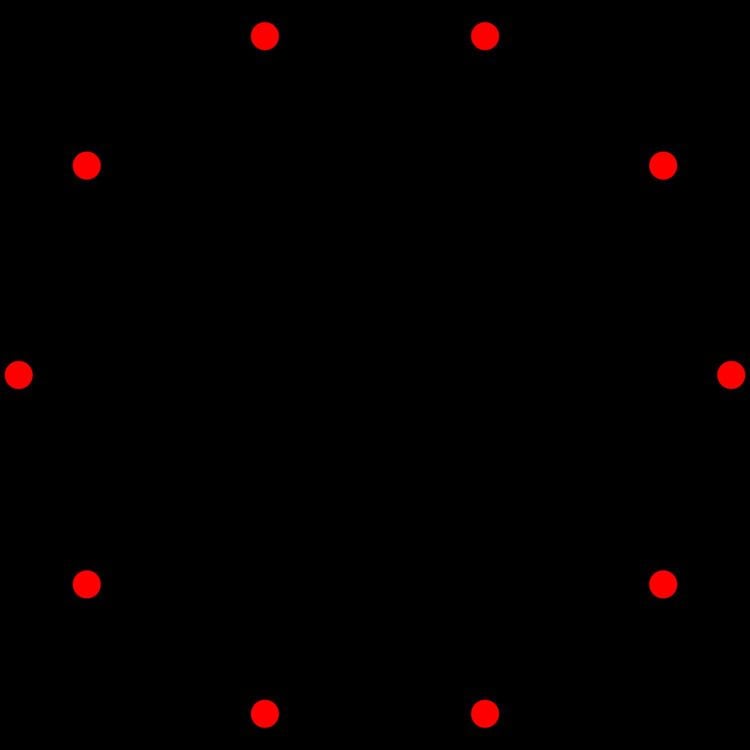
9 simplex

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
9-simplex

In geometry, a 9-simplex is a self-dual regular 9-polytope. It has 10 vertices, 45 edges, 120 triangle faces, 210 tetrahedral cells, 252 5-cell 4-faces, 210 5-simplex 5-faces, 120 6-simplex 6-faces, 45 7-simplex 7-faces, and 10 8-simplex 8-faces. Its dihedral angle is cos−1(1/9), or approximately 83.62°.

It can also be called a decayotton, or deca-9-tope, as a 10-facetted polytope in 9-dimensions.. The name decayotton is derived from deca for ten facets in Greek and -yott (variation of oct for eight), having 8-dimensional facets, and -on.

Coordinates

The Cartesian coordinates of the vertices of an origin-centered regular decayotton having edge length 2 are:

( 1 / 45 ,   1 / 6 ,   1 / 28 ,   1 / 21 ,   1 / 15 ,   1 / 10 ,   1 / 6 ,   1 / 3 ,   ± 1 ) ( 1 / 45 ,   1 / 6 ,   1 / 28 ,   1 / 21 ,   1 / 15 ,   1 / 10 ,   1 / 6 ,   − 2 1 / 3 ,   0 ) ( 1 / 45 ,   1 / 6 ,   1 / 28 ,   1 / 21 ,   1 / 15 ,   1 / 10 ,   − 3 / 2 ,   0 ,   0 ) ( 1 / 45 ,   1 / 6 ,   1 / 28 ,   1 / 21 ,   1 / 15 ,   − 2 2 / 5 ,   0 ,   0 ,   0 ) ( 1 / 45 ,   1 / 6 ,   1 / 28 ,   1 / 21 ,   − 5 / 3 ,   0 ,   0 ,   0 ,   0 ) ( 1 / 45 ,   1 / 6 ,   1 / 28 ,   − 12 / 7 ,   0 ,   0 ,   0 ,   0 ,   0 ) ( 1 / 45 ,   1 / 6 ,   − 7 / 4 ,   0 ,   0 ,   0 ,   0 ,   0 ,   0 ) ( 1 / 45 ,   − 4 / 3 ,   0 ,   0 ,   0 ,   0 ,   0 ,   0 ,   0 ) ( − 3 1 / 5 ,   0 ,   0 ,   0 ,   0 ,   0 ,   0 ,   0 ,   0 )

More simply, the vertices of the 9-simplex can be positioned in 10-space as permutations of (0,0,0,0,0,0,0,0,0,1). This construction is based on facets of the 10-orthoplex.

References

9-simplex Wikipedia
(Text) CC BY-SA