Supriya Ghosh (Editor)

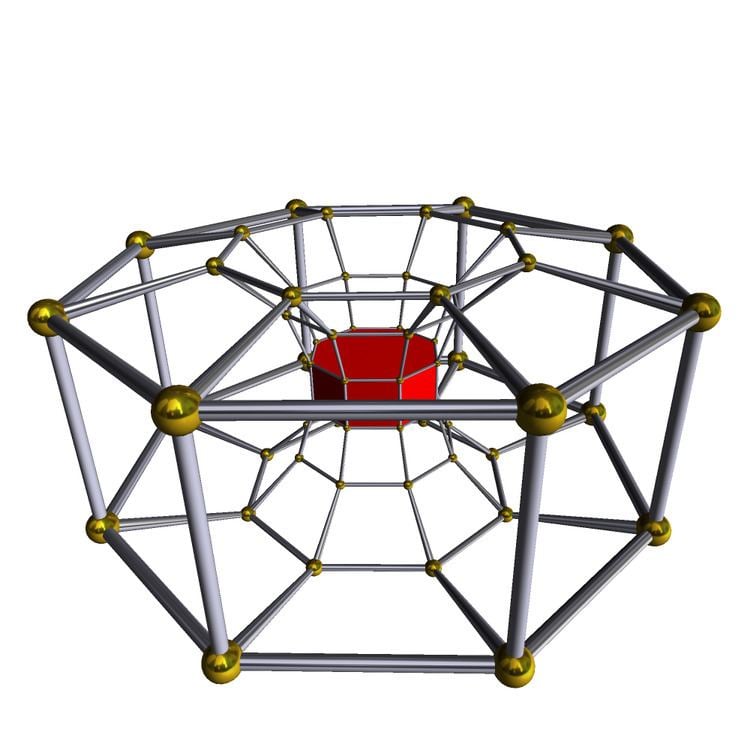
8 8 duoprism

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
8-8 duoprism

In geometry of 4 dimensions, a 8-8 duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two octagons.

Contents

It has 64 vertices, 128 edges, 80 faces (64 squares, and 16 octagons), in 16 octagonal prism cells. It has Coxeter diagram , and symmetry [[8,2,8]], order 512.

Images

The uniform 8-8 duoprism can be constructed from [8]×[8] or [4]×[4] symmetry, order 256 or 64, with extended symmetry doubling these with a 2-fold rotation that maps the two orientations of prisms together. These can be expressed by 4 permutations of uniform coloring of the octahedral prism cells.

Seen in a skew 2D orthogonal projection, it has the same vertex positions as the hexicated 7-simplex, except for a center vertex. The projected rhombi and squares are also shown in the Ammann–Beenker tiling.

The regular complex polytope 8{4}2, , in C 2 has a real representation as a 8-8 duoprism in 4-dimensional space. 8{4}2 has 64 vertices, and 16 8-edges. Its symmetry is 8[4]2, order 128.

It also has a lower symmetry construction, , or 8{}×8{}, with symmetry 8[2]8, order 64. This is the symmetry if the red and blue 8-edges are considered distinct.

8-8 duopyramid

The dual of a 8-8 duoprism is called a 8-8 duopyramid. It has 64 tetragonal disphenoid cells, 128 triangular faces, 80 edges, and 16 vertices.

The regular complex polygon 2{4}8 has 16 vertices in C 2 with a real represention in R 4 matching the same vertex arrangement of the 8-8 duopyramid. It has 64 2-edges corresponding to the connecting edges of the 8-8 duopyramid, while the 16 edges connecting the two octagons are not included.

The vertices and edges makes a complete bipartite graph with each vertex from one octagon is connected to every vertex on the other.

References

8-8 duoprism Wikipedia
(Text) CC BY-SA